《2025年新课程示径学案作业设计九年级物理全一册苏科版》

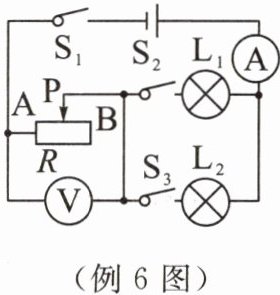
例 6 在如图所示的电路中,电源电压为 9 V 且恒定不变,电流表的量程为 $ 0 \sim 0.6 $ A,电压表的量程为 $ 0 \sim 3 $ V,小灯泡的规格分别为 $ L_1 $“9 V 1.8 W”和 $ L_2 $“9 V 0.9 W”,滑动变阻器 R 的规格为“50 Ω 1.5 A”,不计温度对灯丝电阻的影响.
(1) 求小灯泡 $ L_1 $ 的电阻;
(2) 当滑动变阻器的滑片 P 滑至 a 端,闭合 $ S_1 $、$ S_2 $、$ S_3 $ 时,求电流表的示数;
(3) 当闭合开关 $ S_1 $、$ S_2 $,断开 $ S_3 $ 时,调节滑动变阻器的滑片 P,使小灯泡 $ L_1 $ 的实际功率为 0.8 W,则滑动变阻器消耗的电功率是多少?
(4) 若两个小灯泡中只允许一个工作,且要求电路元件安全使用,在滑片 P 移动的过程中,整个电路消耗的最小电功率是多少?

答案：
(1) $R_{1}=\frac{U_{1额}^{2}}{P_{1额}}=\frac{(9\,V)^{2}}{1.8\,W}=45\,\Omega$
(2) 滑片在a端时，$R=0\,\Omega$；闭合$S_1$、$S_2$、$S_3$，$L_1$与$L_2$并联。
$I_{1额}=\frac{P_{1额}}{U_{1额}}=\frac{1.8\,W}{9\,V}=0.2\,A$，$I_{2额}=\frac{P_{2额}}{U_{2额}}=\frac{0.9\,W}{9\,V}=0.1\,A$
$I=I_{1额}+I_{2额}=0.2\,A+0.1\,A=0.3\,A$
(3) 闭合$S_1$、$S_2$，断开$S_3$，$L_1$与$R$串联。
$U_{1实}=\sqrt{P_{1实}R_{1}}=\sqrt{0.8\,W×45\,\Omega}=6\,V$，$I=\frac{U_{1实}}{R_{1}}=\frac{6\,V}{45\,\Omega}=\frac{2}{15}\,A$
$U_{R}=U-U_{1实}=9\,V-6\,V=3\,V$，$P_{R}=U_{R}I=3\,V×\frac{2}{15}\,A=0.4\,W$
(4) 只L1工作：$L_1$与$R$串联，$U_{R}\leq3\,V$，$U_{1}=9\,V-3\,V=6\,V$，$I_{1}=\frac{6\,V}{45\,\Omega}=\frac{2}{15}\,A$，$P_{总1}=9\,V×\frac{2}{15}\,A=1.2\,W$
只L2工作：$R_{2}=\frac{(9\,V)^{2}}{0.9\,W}=90\,\Omega$，$U_{R}\leq3\,V$，$U_{2}=6\,V$，$I_{2}=\frac{6\,V}{90\,\Omega}=\frac{1}{15}\,A$，$P_{总2}=9\,V×\frac{1}{15}\,A=0.6\,W$
最小总功率为$0.6\,W$
(1) 45Ω
(2) 0.3A
(3) 0.4W
(4) 0.6W

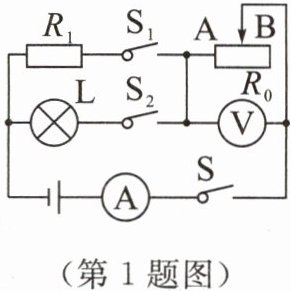
1. 如图所示,电源电压为 6 V,小灯泡 L 上标有“4 V 1.6 W”字样,定值电阻 $ R_1 = 20 \Omega $,不考虑温度对灯丝电阻的影响,滑动变阻器 $ R_0 $ 上标有“20 Ω 1 A”字样.
(1) 小灯泡的电阻为多大?
(2) 若只闭合开关 $ S $、$ S_1 $,要使电路消耗的功率最小,此时滑动变阻器的滑片应向哪端移动? 消耗的最小功率是多少?
(3) 若电流表的测量范围为 $ 0 \sim 0.6 $ A,电压表的测量范围为 $ 0 \sim 3 $ V,当只闭合开关 S 与 $ S_2 $ 时,在不损坏用电器的前提下,求滑动变阻器的调节范围.

答案：
(1) 由 $ P = \frac{U^2}{R} $ 得，小灯泡电阻 $ R_L = \frac{U_{额}^2}{P_{额}} = \frac{(4\,V)^2}{1.6\,W} = 10\,\Omega $。
(2) 只闭合 $ S $、$ S_1 $ 时，$ R_1 $ 与 $ R_0 $ 串联，总功率 $ P = \frac{U^2}{R_{总}} $，电源电压 $ U = 6\,V $ 恒定，要使 $ P $ 最小，需 $ R_{总} $ 最大，即 $ R_0 $ 接入电阻最大。滑片向 B 端移动时 $ R_0 $ 接入电阻最大（20Ω）。此时 $ R_{总} = R_1 + R_0 = 20\,\Omega + 20\,\Omega = 40\,\Omega $，最小功率 $ P_{min} = \frac{U^2}{R_{总}} = \frac{(6\,V)^2}{40\,\Omega} = 0.9\,W $。
(3) 只闭合 $ S $、$ S_2 $ 时，$ L $ 与 $ R_0 $ 串联。灯泡额定电流 $ I_{额} = \frac{P_{额}}{U_{额}} = \frac{1.6\,W}{4\,V} = 0.4\,A $，电流表量程 $ 0 \sim 0.6\,A $，故电路最大电流 $ I_{max} = 0.4\,A $。此时总电阻 $ R_{总} = \frac{U}{I_{max}} = \frac{6\,V}{0.4\,A} = 15\,\Omega $，$ R_0 $ 最小阻值 $ R_{0\,min} = R_{总} - R_L = 15\,\Omega - 10\,\Omega = 5\,\Omega $。电压表测 $ R_0 $ 电压，最大 $ 3\,V $，此时 $ U_L = 6\,V - 3\,V = 3\,V $，电流 $ I = \frac{U_L}{R_L} = \frac{3\,V}{10\,\Omega} = 0.3\,A $，总电阻 $ R_{总}' = \frac{U}{I} = 20\,\Omega $，$ R_0 $ 最大阻值 $ R_{0\,max} = R_{总}' - R_L = 20\,\Omega - 10\,\Omega = 10\,\Omega $。故 $ R_0 $ 调节范围为 $ 5\,\Omega \sim 10\,\Omega $。
(1) $ 10\,\Omega $
(2) 向 B 端移动；$ 0.9\,W $
(3) $ 5\,\Omega \sim 10\,\Omega $

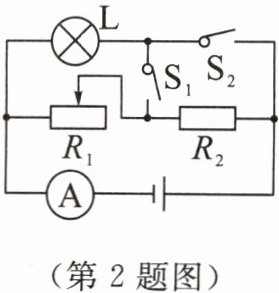
2. 如图所示,电源电压恒定,小灯泡上标有“6 V 3 W”字样,定值电阻 $ R_2 $ 的阻值为 10 Ω,$ R_1 $ 为滑动变阻器,开关 $ S_1 $、$ S_2 $ 都闭合时,L 恰好正常发光,电流表示数为 1.1 A.求:
(1) 小灯泡正常发光时的电阻;
(2) $ S_1 $、$ S_2 $ 都闭合时,$ R_1 $ 在 10 min 内消耗的电能;
(3) $ S_1 $、$ S_2 $ 都断开,调节滑片使 $ R_2 $ 的电功率为 $ R_1 $ 的电功率的 2 倍时,$ R_2 $ 的电功率.

答案：
(1)由 $P=UI=\frac{U^2}{R}$ 可得，小灯泡正常发光时的电阻：$R_L =\frac{U_L^2}{P_L}=\frac{(6V)^2}{3W}=12\Omega$；
(2)由图知，当 $S_1$、$S_2$ 都闭合时，$R_1$ 与 $L$ 并联，$R_2$ 未接入电路，
由 $P=UI$ 可得，小灯泡正常发光时通过的电流：$I_L=\frac{P_L}{U_L}=\frac{3W}{6V}=0.5A$，
由并联电路的电流特点可得，此时通过 $R_1$ 的电流：$I_1=I-I_L=1.1A-0.5A=0.6A$，
因并联电路中各支路两端的电压相等，且 $L$ 恰好正常发光，所以电源电压：$U=U_L=6V$，
$R_1$ 在 $10min$ 内消耗的电能：$W_1=UI_1t=6V×0.6A×10×60s=2160J$；
(3)$S_1$、$S_2$ 都断开，$R_1$ 与 $R_2$ 串联，
因串联电路中各处的电流相等，且 $R_2$ 的电功率为 $R_1$ 的电功率的 2 倍，
所以，由 $P=UI=I^2R$ 可得，$\frac{P_2}{P_1}=\frac{I^2R_2}{I^2R_1}=\frac{R_2}{R_1}=2$，即 $R_1=\frac{1}{2}R_2=\frac{1}{2}×10\Omega=5\Omega$，
因串联电路中总电阻等于各分电阻之和，
所以，电路中的电流：$I'=\frac{U}{R_1+R_2}=\frac{6V}{5\Omega+10\Omega}=0.4A$，
则 $R_2$ 的电功率：$P_2=(I')^2R_2=(0.4A)^2×10\Omega=1.6W$。