《2025年同步实践评价课程基础训练七年级数学上册人教版长沙专版》

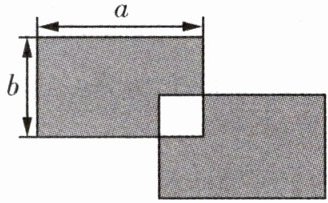
15. 如图,两个形状、大小完全相同的长方形一部分重叠在一起,重叠部分是边长为 $2$ 的正方形,则阴影部分的面积是$2ab-8$(用含 $a,b$ 的代数式表示).

答案： $2ab-8$

16. 魔术表演风靡全国,小明也学起了魔术,发明了一个魔术盒,当任意数对 $(a,b)$ 进入其中时,会得到一个新的数 $a^{2} + b - 1$,例如把 $(3,-2)$ 放入其中,就会得到 $3^{2} + (-2) - 1 = 6$. 现将数对 $(-1,3)$ 放入其中,得到的数是3.

答案： 3

17. 列代数式：
(1)$m,n$ 的绝对值的和的相反数；
(2)$a,b$ 两数平方的差与它们和的平方的商；
(3)$a$ 的倒数的 $70\%$ 与 $b$ 的 $2$ 倍的倒数的和.

答案： 解：（1）$m$，$n$的绝对值的和的相反数为$-(|m|+|n|)$.
（2）$a$，$b$两数平方的差与它们和的平方的商为$\frac{a^2-b^2}{(a+b)^2}$.
（3）$a$的倒数的$70\%$与$b$的2倍的倒数的和为$\frac{70\%}{a}+\frac{1}{2b}$.

18. 已知 $|a| = 3$,$b^{2} = 16$,且 $a,b$ 在原点的两侧,求 $a + b$ 的值.

答案： 解：因为$|a|=3$，$b^2=16$，所以$a=\pm3$，$b=\pm4$. 因为$a$，$b$在原点的两侧，所以$a=3$，$b=-4$或$a=-3$，$b=4$. 当$a=3$，$b=-4$时，$a+b=3+(-4)=-1$；当$a=-3$，$b=4$时，$a+b=-3+4=1$. 所以$a+b$的值为1或$-1$.

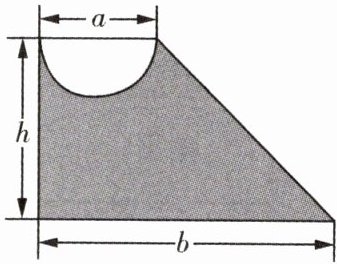
19. 观察下图,回答下列问题：
(1)用代数式表示图中阴影部分的面积；
(2)当 $a = 10cm$,$b = 25cm$,$h = 15cm$ 时,求阴影部分的面积. ($\pi$ 取 $3.14$)

答案： 解：（1）$\frac{1}{2}h(a+b)-\frac{1}{8}\pi a^2$
（2）$\frac{1}{2}h(a+b)-\frac{1}{8}\pi a^2\approx\frac{1}{2}×15×(10+25)-\frac{1}{8}×3.14×10^2=223.25(cm^2)$.