《2025年同步实践评价课程基础训练七年级数学上册人教版长沙专版》

9. 如图,直线有多少条？把它们分别表示出来. 线段有多少条？把它们分别表示出来. 射线有多少条？可以用图中字母表示的射线有多少条？把它们分别表示出来.

答案： 直线有 3 条，分别为直线 AB，直线 AC，直线 BC；线段有 6 条，分别为线段 AB，线段 AC，线段 AD，线段 BD，线段 CD，线段 BC；射线有 14 条，可以用图中字母表示的射线有 8 条，分别为射线 AB，射线 AC，射线 BA，射线 BC，射线 CA，射线 CB，射线 DB，射线 DC.

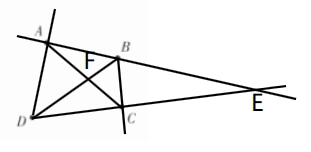
10. 如图,在平面上有四个点$A$,$B$,$C$,$D$,根据下列语句画图：
(1)作射线$BC$；
(2)连接$AC$,$BD$,两条线段交于点$F$；
(3)画直线$AB$,交线段$DC的延长线于点E$；
(4)连接$AD$,并将线段$AD$反向延长.

答案：

11. 探究归纳.
(1)如图①,直线上有$A$,$B$两点,图中有线段1条.

(2)图②的直线上有$A$,$B$,$C$三个点,以$A$为端点,有线段$AB$,线段$AC$；同样以$C$为端点,有线段$CA$,线段$CB$；以$B$为端点,有线段$BA$,线段$BC$. 去除重复线段,图②中共有3条线段. 同样方法探究出图③中共有6条线段.
(3)如果直线上有$n$($n$为正整数)个点,则共有$\frac{n(n-1)}{2}$条线段(用含$n$的式子表示).
(4)往返于甲、乙两地的客车,中途有三个站(如图). 其中每两站的票价不同. 问：

①有多少种不同的票价？
②要准备多少种车票？
①10 种票价. ②20 种车票.

答案：
(1)1
(2)3 6
(3)$\frac{n(n-1)}{2}$
(4)①10 种票价. ②20 种车票.

12. 如图,$3条直线两两相交最多有3$个交点,$4条直线两两相交最多有6$个交点. 按照这样的规律,$20$条直线两两相交最多有190个交点.

答案： 190