《2025年同步实践评价课程基础训练七年级数学上册人教版长沙专版》

23. 某商场销售一种夹克衫和 $T$ 恤,夹克衫每件定价为 $100$ 元,$T$ 恤每件定价为 $50$ 元,该商场在开展促销活动期间,向顾客提供两种优惠方案.
方案一：买一件夹克衫送一件 $T$ 恤；
方案二：夹克衫和 $T$ 恤均按定价的 $80\%$ 出售.
现有顾客要到该商场购买夹克衫 $30$ 件,$T$ 恤 $x$ 件 $(x ＞ 30)$.
(1)若用方案一购买夹克衫需付款3000元,$T$ 恤需付款50(x-30)元；若用方案二购买夹克衫需付款2400元,$T$ 恤需付款40x元.
(2)按方案一购买夹克衫和 $T$ 恤共需付款1500+50x元；按方案二购买夹克衫和 $T$ 恤共需付款2400+40x元.
(3)某公司想买 $T$ 恤 $60$ 件,$90$ 件,$100$ 件时,请通过计算说明分别采用哪种方案更加划算.
买60件时，采用方案一划算；买90件时，两种方案一样；买100件时，采用方案二划算.

答案： 解：（1）3000 50$(x-30)$ 2400 40$x$
（2）$1500+50x$ $2400+40x$
（3）买60件时，采用方案一划算；买90件时，两种方案一样；买100件时，采用方案二划算.

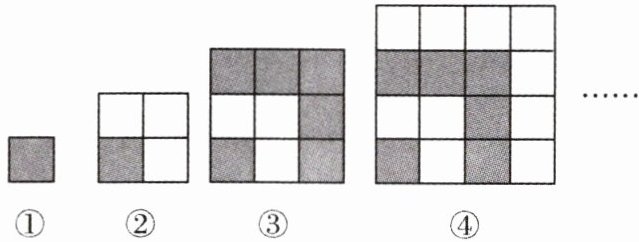
24. 用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第①个图形有 $1$ 个小正方形；
第②个图形有 $1 + 3 = 4$ 个小正方形；
第③个图形有 $1 + 3 + 5 = 9$ 个小正方形；
第④个图形有 $1 + 3 + 5 + 7 = 16$ 小正方形；
……

(1)根据上面的发现我们可以猜想：$1 + 3 + 5 + 7 + … + (2n - 1) = $$n^2$ (用含 $n$ 的代数式表示).
(2)请根据你的发现计算：
①$1 + 3 + 5 + 7 + … + 99$；
②$101 + 103 + 105 + … + 199$.
①$2500$；②$7500$

答案： 解：（1）因为第①个图形有1个小正方形；第②个图形有$1+3=4$（个）小正方形；第③个图形有$1+3+5=9$（个）小正方形；第④个图形有$1+3+5+7=16$（个）小正方形……所以$1+3+5+7+\cdots+(2n-1)=\left(\frac{1+2n-1}{2}\right)^2=n^2$.
（2）①$1+3+5+7+\cdots+99=\left(\frac{1+99}{2}\right)^2=50^2=2500$；②因为$1+3+5+7+\cdots+199=\left(\frac{1+199}{2}\right)^2=10000$，所以$101+103+105+\cdots+199=10000-2500=7500$.