第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 下列说法中,正确的是(
A.符号不同的两个数互为相反数
B.有理数 $ a $ 一定比它的相反数 $ -a $ 大
C.若 $ a $,$ b $ 互为相反数,则 $ a + b = 0 $
D.互为相反数的两个数一定位于原点的左右两侧
C
)A.符号不同的两个数互为相反数
B.有理数 $ a $ 一定比它的相反数 $ -a $ 大
C.若 $ a $,$ b $ 互为相反数,则 $ a + b = 0 $
D.互为相反数的两个数一定位于原点的左右两侧
答案:
C
2. 如图,数轴上点 $ A $ 表示的数是 $ 2024 $,$ OA = OB $,则点 $ B $ 表示的数是(
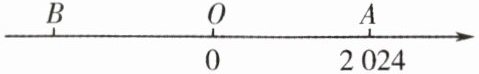
A.$ 2024 $
B.$ -2024 $
C.$ \dfrac{1}{2024} $
D.$ -\dfrac{1}{2024} $
B
)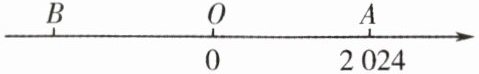
A.$ 2024 $
B.$ -2024 $
C.$ \dfrac{1}{2024} $
D.$ -\dfrac{1}{2024} $
答案:
B
3. 已知 $ 3m $ 与 $ -6 $ 互为相反数,则 $ m $ 的值为(
A.$ 1 $
B.$ 2 $
C.$ -2 $
D.$ -3 $
B
)A.$ 1 $
B.$ 2 $
C.$ -2 $
D.$ -3 $
答案:
B
4. 化简:(1)$ -[-(+3)] = $
3
;(2)$ +\left[-\left(+2\dfrac{1}{2}\right)\right] = $$-2\frac{1}{2}$
.
答案:
(1)3
(2)$-2\frac{1}{2}$
(1)3
(2)$-2\frac{1}{2}$
5. 若 $ x $ 和 $ y $ 互为相反数,则 $ 2025 + 2x + 2y = $
2025
.
答案:
2025
6. 写出下列各数的相反数:
$ -\dfrac{2}{3} $,$ 0.618 $,$ 2035 $,$ 0 $,$ -100 $,$ -(-2) $.
$ -\dfrac{2}{3} $,$ 0.618 $,$ 2035 $,$ 0 $,$ -100 $,$ -(-2) $.
答案:
解:它们的相反数分别为$\frac{2}{3}$,$-0.618$,$-2035$,0,100,$-2$.
7. 已知表示数 $ a $ 的点在数轴上的位置如图所示.

(1)在数轴上表示出 $ a $ 的相反数的位置;
(2)若数 $ a $ 与其相反数相距 $ 20 $ 个单位长度,则 $ a $ 表示的数是多少?
(3)在(2)的条件下,若表示数 $ b $ 的点与数 $ a $ 的相反数表示的点相距 $ 5 $ 个单位长度,则 $ b $ 表示的数是多少?

(1)在数轴上表示出 $ a $ 的相反数的位置;
(2)若数 $ a $ 与其相反数相距 $ 20 $ 个单位长度,则 $ a $ 表示的数是多少?
(3)在(2)的条件下,若表示数 $ b $ 的点与数 $ a $ 的相反数表示的点相距 $ 5 $ 个单位长度,则 $ b $ 表示的数是多少?
答案:
(1)
(2)$-10$
(3)5或15
(1)

(2)$-10$
(3)5或15
查看更多完整答案,请扫码查看


