《2025年同步实践评价课程基础训练七年级数学上册人教版长沙专版》

7. 与时间的计量方式一样,角的度、分、秒也是六十进制的,六十进制记数法起源于四大文明古国之一的古巴比伦. 下列各式中的角度互化正确的是(D)
A.$63.5^{\circ}=63^{\circ}50'$
B.$23^{\circ}12'36''= 23.48^{\circ}$
C.$18^{\circ}18'18''= 18.33^{\circ}$
D.$22.25^{\circ}=22^{\circ}15'$

答案： D

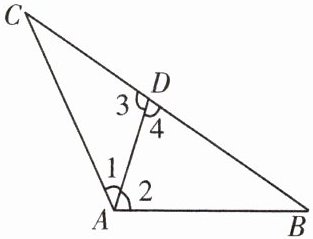
8. 如图,写出符合下列条件的角(图中所有的角均指小于平角的角).
(1)能用一个大写字母表示的角；
(2)以点 $A$ 为顶点的角；
(3)图中所有的角(可用简便方法表示).

答案：
(1)∠B，∠C.
(2)∠CAD，∠BAD，∠BAC.
(3)∠C，∠B，∠1，∠2，∠3，∠4，∠CAB.

9. 钟面上的角度问题.
(1)某校七年级在下午 $3:00$ 开展“阳光体育”活动,下午 $3:00$ 这一时刻,时钟上分针与时针所夹的小于平角的角等于90$^{\circ}$.
(2)下午 6 时 20 分,时针与分针所夹的小于平角的角为70$^{\circ}$.
(3)从 12 时整开始,至少再过多少时间,分针与时针再一次重合？
设至少再过x min 分针与时针再一次重合.由题意，得0.5x+360=6x，解得x=720/11，所以从12时整开始，至少再过720/11min，分针与时针再一次重合.

答案：
(1)90
(2)70
(3)设至少再过x min 分针与时针再一次重合.由题意，得0.5x+360=6x，解得x=720/11，所以从12时整开始，至少再过720/11min，分针与时针再一次重合.

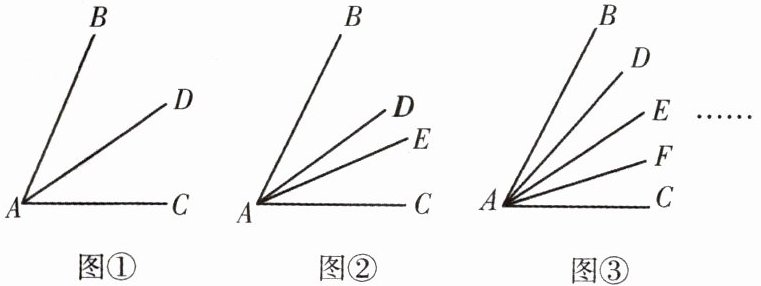
10. 观察下列图形,回答问题.
(1)如图①,在角的内部作 1 条射线,那么图中一共有3个角；
(2)如图②,在角的内部作 2 条射线,那么图中一共有6个角；
(3)如图③,在角的内部作 3 条射线,那么图中一共有10个角；
(4)在角的内部作 $n$ 条射线,那么图中一共有(n+2)(n+1)/2个角.
【变式】以直线 $l$ 外一点 $P$ 为端点,向直线 $l$ 上的 $n(n＞1)$ 个点作射线,则以点 $P$ 为顶点,以这些射线为边的角(小于 $180^{\circ}$)的个数为n(n-1)/2.(用含有 $n$ 的式子表示)

答案：
(1)3
(2)6
(3)10
(4)(n+2)(n+1)/2【变式】n(n-1)/2