《2025年同步解析与测评学考练八年级数学上册人教版》

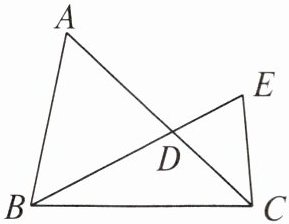
3. 图中共有5个三角形,以BC为边的三角形共有3个,以∠E为内角的三角形共有2个。

答案： 5 3 2 【解析】图中三角形有△ABD，△BCD，△CDE，△ABC，△BCE，共 5 个；以 BC 为边的三角形有△BCD，△ABC，△BCE，共 3 个；以∠E 为内角的三角形有△CDE，△BCE，共 2 个.

4. 如图,将房屋屋顶的框架抽象成一个几何图形,几何图形中一共有多少个三角形？写出这些三角形。

答案： 【解】图中共有 10 个三角形，分别是△BDF，△BDA，△BEA，△BCA，△DFA，△EDA，△EGA，△CGE，△ACE，△ACD.

5. 如图,在直角三角形ABC中,∠A = 90°,∠B = 30°。动点P从点C出发,沿边CB,BA向点A运动。在点P运动过程中,△PAC可能成为的特殊三角形依次是(C)

A.直角三角形→等边三角形→直角三角形→等边三角形→直角三角形
B.等腰三角形→直角三角形→等边三角形→直角三角形→等腰直角三角形
C.直角三角形→等边三角形→直角三角形→等腰直角三角形→直角三角形
D.等腰直角三角形→等腰三角形→直角三角形→等腰直角三角形→直角三角形

答案： C 【解析】根据特殊三角形的定义，在点 P 运动过程中，逐一画图分析获解，可知△PAC 可能成为的特殊三角形依次是直角三角形→等边三角形→直角三角形→等腰直角三角形→直角三角形，故选 C.

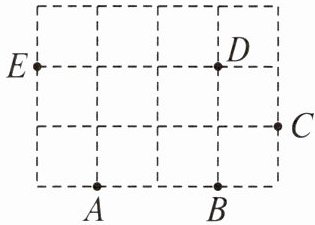
6. 如图,在方格纸中,过A,B,C,D,E五个格点中任意三点画三角形。
- (1) 请写出以点D,E,C为顶点的三角形的内角。
- (2) 以AB为边能画出哪几个三角形？
- (3) 分别指出(2)中的等腰三角形和钝角三角形。

答案：
【解】
(1)∠EDC，∠DEC，∠ECD；
(2)如图，以 AB 为边可以画出 3 个三角形：△ABE，△ABD，△ABC；
(3)如图，△ABD 是等腰三角形，△ABE 与△ABC 是钝角三角形.

7. 三角形纸片内有200个点,连同三角形的顶点共203个点,其中任意三点都不共线。现以这些点为顶点画三角形,并把纸片剪成小三角形,剪出的小三角形的个数是(401)
A.399
B.401
C.405
D.407

答案： B 【解析】根据题意可以得到当三角形纸片内有 1 个点时，可剪出 3 个小三角形；当有 2 个点时，可剪出 5 个小三角形；当有 3 个点时，可剪出 7 个三角形，因而若有 n 个点时，可剪出(2n+1)个三角形.根据题意，可剪出的三角形的个数为 2n+1=2×200+1=401.