《2025年一阅优品作业本九年级数学全一册人教版》

12. 点M(cos30°,sin30°)关于原点中心对称的点的坐标为 ( )

A.($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)
B.(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$)
C.(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)
D.(-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$)

答案： D

13. 计算：
(1)3tan30°-2tan45°+2cos30°= ______.
$(2)cos^270°+cos45°·sin45°+sin^270°= ______.$

答案： （1）$2\sqrt{3}-2$
（2）$\frac{3}{2}$

14. 若2cos30°-3tanα= 0,则锐角α的度数为______.

答案： 30°

15. 化简：|tan60°-2|= ______.

答案： $2-\sqrt{3}$

16. 已知tan^2α-(1+$\sqrt{3}$)tanα+$\sqrt{3}$= 0,求锐角α的度数.

答案： 等式化简，得$(\tan\alpha-1)(\tan\alpha-\sqrt{3})=0$.
∴$\tan\alpha=1$或$\tan\alpha=\sqrt{3}$.
∴$\alpha=45^\circ$或$\alpha=60^\circ$.

17. 对于钝角α,定义它的三角函数值如下：sinα= sin(180°-α),cosα= -cos(180°-α).求sin120°,cos120°,sin150°的值.

答案： $\sin120^\circ=\sin(180^\circ-120^\circ)=\sin60^\circ=\frac{\sqrt{3}}{2}$.
$\cos120^\circ=-\cos(180^\circ-120^\circ)=-\cos60^\circ=-\frac{1}{2}$.
$\sin150^\circ=\sin(180^\circ-150^\circ)=\sin30^\circ=\frac{1}{2}$.

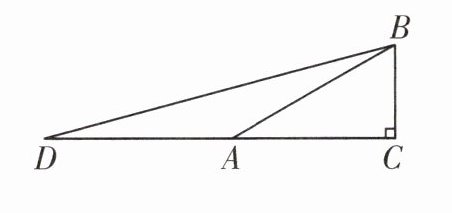
18. 如图,在Rt△ABC中,∠C= 90°,∠BAC= 30°,延长CA至点D,使AD= AB.
(1)求∠D的度数.
(2)求tanD的值.
(3)请用类似的方法,求tan22.5°.

答案： （1）
∵$AD=AB$，
∴$\angle D=\angle ABD$.
∴$\angle D=\frac{1}{2}\angle BAC=15^\circ$.
（2）设$BC=a(a＞0)$.
∵$\angle C=90^\circ$，$\angle BAC=30^\circ$，
∴$AB=AD=2a$，$AC=\sqrt{3}a$.
∴$\tan D=\frac{BC}{DC}=\frac{BC}{AD+AC}=\frac{a}{(2+\sqrt{3})a}=2-\sqrt{3}$.
（3）构造等腰直角三角形ABC，$AC=BC$，延长CA至点D，使$AD=AB$，则$\angle D=22.5^\circ$.
设$BC=b(b＞0)$，则$AC=b$，$AB=AD=\sqrt{2}b$.
∴$\tan22.5^\circ=\frac{BC}{CD}=\frac{BC}{AD+AC}=\frac{b}{(\sqrt{2}+1)b}=\sqrt{2}-1$.