《2025年一阅优品作业本九年级数学全一册人教版》

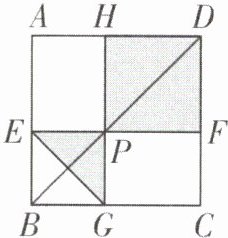
·母题9:(2023·仙居期末)如图,某校计划在边长为10米的正方形花坛ABCD内种花,过BD上一点P作 $ EF// BC $,$ GH// AB $,分别交正方形ABCD的四边于点E,F,G,H,连接EG,在$ \triangle EGP $区域种百合花,在四边形HPFD区域种玫瑰花.若种植百合花的成本为20元/$ m^{2} $,玫瑰花的成本为15元/$ m^{2} $,则种植两种花卉的计划成本最少为______元.

答案： 600

8. 高尔夫球运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)之间关系的部分数据如下表所示.
| x/s | ... | 0.5 | 1 | 1.5 | 2 | ... |
| y/m | ... | 8.75 | 15 | 18.75 | 20 | ... |
(1)根据表格信息,有下列三个函数关系式:① $ y= \frac{25}{2}x+\frac{5}{2} $;② $ y= \frac{15}{x} $;③ $ y= -5x^{2}+20x $.其中刻画y与x的关系最准确的是______.(填序号)
(2)利用题(1)中选取的函数关系式,分析小球经过多少秒落回地面.

答案：
(1)③
(2)令$y=-5x^{2}+20x=0$，解得$x_{1}=0$，$x_{2}=4$.
∴小球经过4秒落回地面.

9. 某商品现在的售价为每件60元,每星期可卖出300件,市场调查发现:如调整价格,每涨价1元,每星期要少卖出10件.已知商品的进价为每件40元.
(1)若每件涨价x元,每周卖出y件,求y与x的函数解析式.
(2)若每周可获利w元,求w与x的函数解析式.
(3)如何定价才能使利润最大? 请求出最大利润.

答案：
(1)根据题意，得$y=300-10x$.
(2)$w=(60-40+x)(300-10x)=-10x^{2}+100x+6000=-10(x-5)^{2}+6250$.
(3)由题
(2)可知，当$x=5$时，w有最大值，为6250.
此时售价为$60+5=65$（元）.
答：每件定价为65元时，利润最大，最大利润为6250元.