《2025年一阅优品作业本九年级数学全一册人教版》

7. 如图,C是线段AB上的一个动点,AB= 1,分别以AC和CB为一边作正方形,用S表示这两个正方形的面积之和,下列判断正确的是 ( )


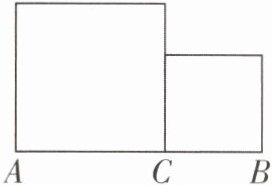
A.当C是AB的中点时,S最小
B.当C是AB的中点时,S最大
C.当C是AB的三等分点时,S最小
D.当C是AB的三等分点时,S最大

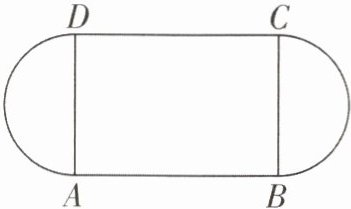
答案： A

8. 下图是一个400米跑道的示意图,两对边是半圆,中间的足球场ABCD是矩形,设直道AB的长为x米.
(1)请用含x的代数式表示边BC.
(2)设矩形ABCD的面积为S.
① 求出S关于x的函数解析式；
② 当直道AB的长为多少米时,矩形ABCD的面积最大?

答案： （1）由题意，得$\frac{1}{2}\pi\cdot BC=\frac{400 - 2x}{2}$.
$\therefore BC=\frac{400 - 2x}{\pi}$.
（2）① $\because$ 四边形ABCD是矩形，
$\therefore S=\frac{400 - 2x}{\pi}\cdot x=-\frac{2}{\pi}(x - 100)^{2}+\frac{20000}{\pi}$.
② 当$x = 100$时，S最大，即当直道AB的长为100米时，矩形ABCD的面积最大.

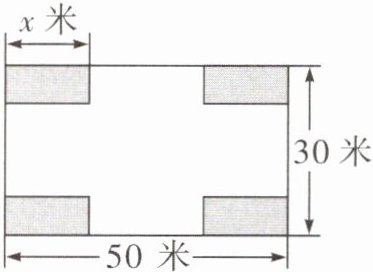
9. 某社区决定把一块长为50米,宽为30米的矩形空地建成居民健身广场.设计方案如图,涂色区域是绿化区(四块绿化区是大小、形状都相同的矩形),空白区域是活动区,且四周的4个出口宽度相同,其宽度不小于14米,不大于26米.设绿化区较长边的长为x米,活动区的面积为y平方米.为了知道绿化区宽度的取值范围,小明同学根据出口宽度不小于14米,算出x≤18.
(1)求y与x的函数解析式,并直接写出自变量x的取值范围.
(2)求活动区的最大面积.
(3)预计活动区造价为50元/平方米,绿化区造价为40元/平方米,若社区的此项建造投资费用不得超过72 000元,求投资费用最少时活动区的出口宽度.

答案： （1）根据题意，绿化区的宽为$[30 - (50 - 2x)]÷2=(x - 10)$米.
$\therefore y = 50×30 - 4x(x - 10)= -4x^{2}+40x + 1500(12\leqslant x\leqslant18)$.
（2）$y = -4x^{2}+40x + 1500 = -4(x - 5)^{2}+1600$.
$\because a = -4 ＜ 0$，$\therefore$ 抛物线的开口向下.
$\therefore$ 当$12\leqslant x\leqslant18$时，y随x的增大而减小.
$\therefore$ 当$x = 12$时，$y_{最大}= 1404$.
答：活动区的最大面积为1404平方米.
（3）设投资费用为w元.
由题意，得$w = 50(-4x^{2}+40x + 1500)+40×4x(x - 10)= -40(x - 5)^{2}+76000$.
$\because$ 当$12\leqslant x\leqslant18$时，w随x的增大而减小，
$\therefore$ 当$x = 18$时，$w_{最小}= 69240 ＜ 72000$，符合题意.
此时活动区的出口宽度为$50 - 2x = 50 - 2×18 = 14(米)$.
答：投资费用最少时活动区的出口宽度为14米.