第71页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
11. 若△ABC与$△A_1B_1C_1$的相似比为$2:3,△A_1B_1C_1$与$△A_2B_2C_2$的相似比为2:3,则△ABC与$△A_2B_2C_2$的相似比为______.
答案:
$4:9$
12. 一个四边形的边长分别为2,3,4,6,另一个和它相似的四边形的最短边长为6,则较大多边形的周长为______.
答案:
45
13. 如图,在Rt△ABC中,∠C= 90°,以顶点A为圆心,适当长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于$\frac{1}{2}MN$长为半径画弧,两弧交于点P,射线AP交边BC于点D.若△DAC与△ABC相似,则∠B= ______.
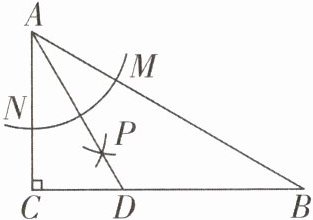

答案:
$30^{\circ}$
14. 如图,在给出的方格内通过放大或缩小画出已给图形的相似图形.
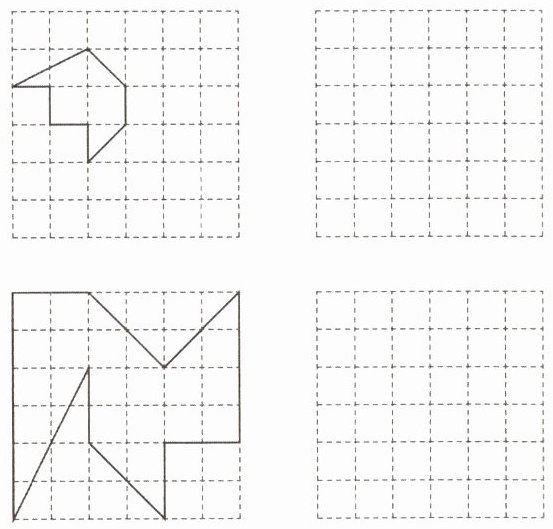

答案:
图①②即为所求作图形.


图①②即为所求作图形.


15. 如图,□ABCD的对角线AC,BD交于点O,E,F,G,H分别是AO,BO,CO,DO的中点,依次连接点E,F,G,H,得到□EFGH.求证:□EFGH∽□ABCD.
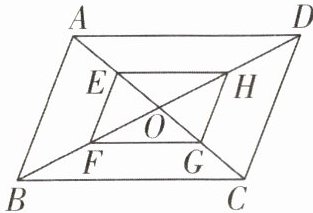

答案:
$\because E,F,G,H$ 分别是 $AO,BO,CO,DO$ 的中点,
$\therefore \frac{EF}{AB}=\frac{FG}{BC}=\frac{GH}{CD}=\frac{EH}{AD}=\frac{1}{2}$.
$\because EF// AB,FG// BC,GH// CD,EH// AD$,
$\therefore \angle FEO=\angle BAO,\angle OEH=\angle OAD$.
$\therefore \angle FEO+\angle OEH=\angle BAO+\angle OAD$,即 $\angle FEH=\angle BAD$.同理,$\angle EFG=\angle ABC,\angle FGH=\angle BCD,\angle GHE=\angle CDA$.
$\therefore □ EFGH\backsim □ ABCD$.
$\therefore \frac{EF}{AB}=\frac{FG}{BC}=\frac{GH}{CD}=\frac{EH}{AD}=\frac{1}{2}$.
$\because EF// AB,FG// BC,GH// CD,EH// AD$,
$\therefore \angle FEO=\angle BAO,\angle OEH=\angle OAD$.
$\therefore \angle FEO+\angle OEH=\angle BAO+\angle OAD$,即 $\angle FEH=\angle BAD$.同理,$\angle EFG=\angle ABC,\angle FGH=\angle BCD,\angle GHE=\angle CDA$.
$\therefore □ EFGH\backsim □ ABCD$.
16. 如图①,点C将线段AB分成两部分,若$AC^{2}= BC\cdot AB(AC>BC)$,则称C是线段AB的黄金分割点.
(1) 求$\frac{AC}{BC}$的值.
(2) 如图②,以AC为边作正方形ACDE,以BC和CD为边作矩形BCDF,则矩形ABFE和矩形BCDF相似吗? 请说明理由.如果相似,写出它们的相似比.
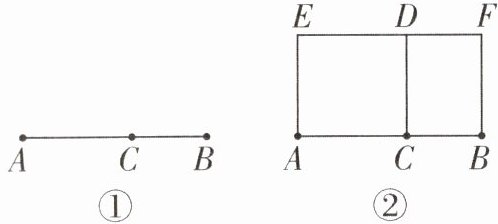
(1) 求$\frac{AC}{BC}$的值.
(2) 如图②,以AC为边作正方形ACDE,以BC和CD为边作矩形BCDF,则矩形ABFE和矩形BCDF相似吗? 请说明理由.如果相似,写出它们的相似比.

答案:
(1)设 $AC=x,BC=1$,则 $AB=x+1$.
由题意,得 $x^{2}=x+1$,解得 $x=\frac{1+\sqrt{5}}{2}$(负值舍去).
$\therefore \frac{AC}{BC}=\frac{\sqrt{5}+1}{2}$.
(2)相似
理由:由 $AC^{2}=BC\cdot AB$,得 $\frac{AC}{BC}=\frac{AB}{AC}$.
$\because AE=AC=BF$,
$\therefore \frac{AE}{BC}=\frac{AB}{BF}=\frac{\sqrt{5}+1}{2}$.
$\because$ 矩形的各内角对应相等,
$\therefore$ 矩形 $ABFE$ 和矩形 $BCDF$ 相似,相似比为 $\frac{\sqrt{5}+1}{2}$.
(1)设 $AC=x,BC=1$,则 $AB=x+1$.
由题意,得 $x^{2}=x+1$,解得 $x=\frac{1+\sqrt{5}}{2}$(负值舍去).
$\therefore \frac{AC}{BC}=\frac{\sqrt{5}+1}{2}$.
(2)相似
理由:由 $AC^{2}=BC\cdot AB$,得 $\frac{AC}{BC}=\frac{AB}{AC}$.
$\because AE=AC=BF$,
$\therefore \frac{AE}{BC}=\frac{AB}{BF}=\frac{\sqrt{5}+1}{2}$.
$\because$ 矩形的各内角对应相等,
$\therefore$ 矩形 $ABFE$ 和矩形 $BCDF$ 相似,相似比为 $\frac{\sqrt{5}+1}{2}$.
查看更多完整答案,请扫码查看


