第50页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
一、切线的性质
·母题:如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP= BP.
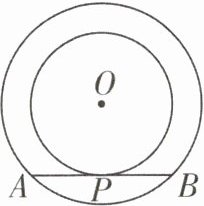
·母题:如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,点P为切点.求证:AP= BP.

答案:
连接OP.
∵AB是小圆的切线,
∴OP⊥AB.在大圆中由垂径定理,得AP=BP.
∵AB是小圆的切线,
∴OP⊥AB.在大圆中由垂径定理,得AP=BP.
·变式1:如图,一个边长为4的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为( )
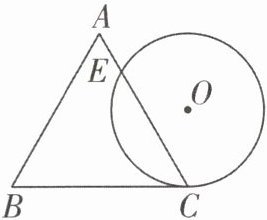
A.$2\sqrt{3}$
B.$\sqrt{3}$
C.2
D.3

A.$2\sqrt{3}$
B.$\sqrt{3}$
C.2
D.3
答案:
变式1:D 解析:如图,连接OC,并过点O作OF⊥CE于点F.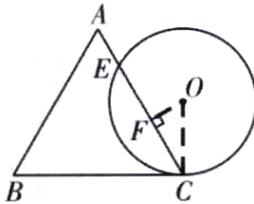
∵△ABC是等边三角形,边长为4,
∴△ABC的高为$2\sqrt{3}$,
∴$OC=\sqrt{3}$.
∵∠OCB=90°,∠ACB=60°,
∴∠OCF=30°.在Rt△OFC中,可得$OF=\frac{1}{2}OC=\frac{\sqrt{3}}{2}$,$FC=\sqrt{3}OF=\frac{3}{2}$.
∴CE=2FC=3.
变式1:D 解析:如图,连接OC,并过点O作OF⊥CE于点F.

∵△ABC是等边三角形,边长为4,
∴△ABC的高为$2\sqrt{3}$,
∴$OC=\sqrt{3}$.
∵∠OCB=90°,∠ACB=60°,
∴∠OCF=30°.在Rt△OFC中,可得$OF=\frac{1}{2}OC=\frac{\sqrt{3}}{2}$,$FC=\sqrt{3}OF=\frac{3}{2}$.
∴CE=2FC=3.
·变式2:如图,AB是⊙O的直径,PQ切⊙O于点T,AC⊥PQ于点C,交⊙O于点D.
(1)求证:AT平分∠BAC.
(2)若AD= 2,TC= $\sqrt{3}$,求⊙O的半径.
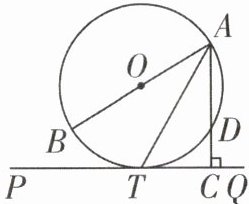
(1)求证:AT平分∠BAC.
(2)若AD= 2,TC= $\sqrt{3}$,求⊙O的半径.
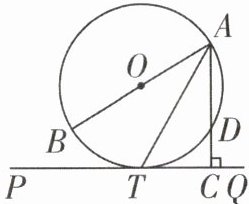
答案:
(1)如图,连接OT.
∵PQ切⊙O于点T,
∴OT⊥PQ.
∵AC⊥PQ,
∴OT//AC,
∴∠TAC=∠ATO.
∵OT=OA,
∴∠ATO=∠TAO.
∴∠TAO=∠TAC,即AT平分∠BAC.
(2)如图,过点O作OM⊥AC于点M.
∴$AM=MD=\frac{1}{2}AD=1$.
∵∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM是矩形,
∴$OM=TC=\sqrt{3}$.在Rt△AOM中,$AO=\sqrt{OM^2+AM^2}=2$.
∴⊙O的半径为2.
(1)如图,连接OT.
∵PQ切⊙O于点T,
∴OT⊥PQ.
∵AC⊥PQ,
∴OT//AC,
∴∠TAC=∠ATO.
∵OT=OA,
∴∠ATO=∠TAO.
∴∠TAO=∠TAC,即AT平分∠BAC.

(2)如图,过点O作OM⊥AC于点M.
∴$AM=MD=\frac{1}{2}AD=1$.
∵∠OTC=∠ACT=∠OMC=90°,
∴四边形OTCM是矩形,
∴$OM=TC=\sqrt{3}$.在Rt△AOM中,$AO=\sqrt{OM^2+AM^2}=2$.
∴⊙O的半径为2.
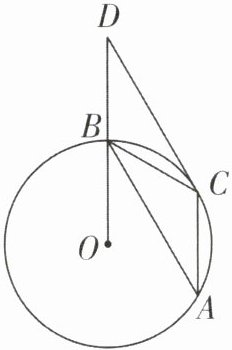
·变式3:如图,⊙O上有A,B,C三点,D是OB延长线上的点,∠BDC= 30°,CD是⊙O的切线,⊙O的半径为$\sqrt{2}$.
(1)求∠A的度数.
(2)如果AC//BD,请判断四边形ACDB是什么四边形,并求其周长.
(1)求∠A的度数.
(2)如果AC//BD,请判断四边形ACDB是什么四边形,并求其周长.

答案:
(1)如图,连接OC.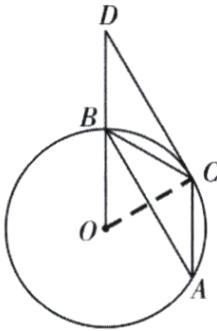
∵CD是⊙O的切线,
∴OC⊥CD,即∠OCD=90°.
∵∠BDC=30°,
∴∠BOC=90° - ∠BDC=60°.
∴$\angle A=\frac{1}{2}\angle BOC=30^\circ$.
(2)四边形ACDB是平行四边形.
∵AC//BD,
∴∠D+∠ACD=180°.
∴∠ACD=150°.
∴∠ACD+∠BAC=180°,
∴AB//CD.
∴四边形ACDB是平行四边形.在Rt△DOC中,∠OCD=90°,∠BDC=30°,
∴$OD=2OC=2\sqrt{2}$,$CD=\sqrt{3}OC=\sqrt{6}$.
∴$BD=OD - OB=\sqrt{2}$.
∴▱ACDB的周长为$2\sqrt{2}+2\sqrt{6}$.
(1)如图,连接OC.

∵CD是⊙O的切线,
∴OC⊥CD,即∠OCD=90°.
∵∠BDC=30°,
∴∠BOC=90° - ∠BDC=60°.
∴$\angle A=\frac{1}{2}\angle BOC=30^\circ$.
(2)四边形ACDB是平行四边形.
∵AC//BD,
∴∠D+∠ACD=180°.
∴∠ACD=150°.
∴∠ACD+∠BAC=180°,
∴AB//CD.
∴四边形ACDB是平行四边形.在Rt△DOC中,∠OCD=90°,∠BDC=30°,
∴$OD=2OC=2\sqrt{2}$,$CD=\sqrt{3}OC=\sqrt{6}$.
∴$BD=OD - OB=\sqrt{2}$.
∴▱ACDB的周长为$2\sqrt{2}+2\sqrt{6}$.
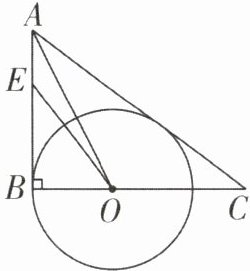
·变式4:如图,在Rt△ABC中,∠B= 90°,E是AB上一点,O是BC上一点,∠C= ∠BEO,以点O为圆心,OB长为半径作⊙O,AC是⊙O的切线.
(1)求证:OE= OC.
(2)若BE= 4,BC= 8,求OE的长.
(1)求证:OE= OC.
(2)若BE= 4,BC= 8,求OE的长.

答案:
(1)如图,设AC切⊙O于点Q,连接OQ.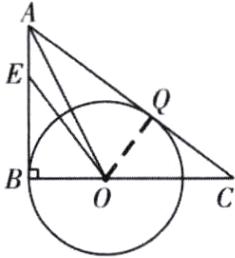
∵AC是⊙O的切线,
∴∠CQO=90°.
∵∠B=∠CQO=90°,∠BEO=∠C,BO=QO,
∴△OBE≌△OQC(AAS),
∴OE=OC.
(2)设OE=OC=x,则BO=BC - OC=8 - x.在Rt△OBE中,$BE^2+BO^2=OE^2$,
∴$4^2+(8 - x)^2=x^2$,
∴x=5,即OE=5.
(1)如图,设AC切⊙O于点Q,连接OQ.

∵AC是⊙O的切线,
∴∠CQO=90°.
∵∠B=∠CQO=90°,∠BEO=∠C,BO=QO,
∴△OBE≌△OQC(AAS),
∴OE=OC.
(2)设OE=OC=x,则BO=BC - OC=8 - x.在Rt△OBE中,$BE^2+BO^2=OE^2$,
∴$4^2+(8 - x)^2=x^2$,
∴x=5,即OE=5.
查看更多完整答案,请扫码查看


