《2025年一阅优品作业本九年级数学全一册人教版》

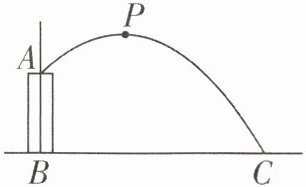
10. 如图,有一个竖直的喷水枪AB,从喷水口A处喷出的水流的运动路线是抛物线.如果水流的最高点P到喷水枪AB所在直线的距离为3 m,且到地面BC的距离为5 m,水流的落地点C到喷水枪底部B的距离为8 m,求喷水枪AB的长度.

答案： 如图，以BC所在直线为x轴，AB所在直线为y轴，建立平面直角坐标系.
由题意，得抛物线的顶点P(3,5)，点C(8,0).
∴设抛物线的解析式为$y=a(x-3)^{2}+5$.
代入点C(8,0)，得$25a+5=0$，解得$a=-\frac{1}{5}$.
∴抛物线的解析式为$y=-\frac{1}{5}(x-3)^{2}+5$.
当$x=0$时，$y=-\frac{1}{5}×(0-3)^{2}+5=3.2$.
即点A的坐标为(0,3.2).
∴AB的长度为3.2m.
答：喷水枪AB的长度为3.2m.

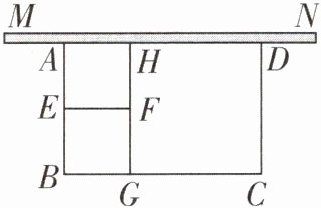
11. 一段长为30 m的墙MN前有一块矩形空地ABCD,用100 m长的篱笆围成如图所示的图形(靠墙的一边不用篱笆,篱笆的厚度忽略不计),其中四边形AEFH和四边形CDHG是矩形,四边形EBGF是边长为10 m的正方形,设 $ CD= x $ m.
(1)若矩形CDHG的面积为 $ 125m^{2} $,求CD的长.
(2)当CD的长为多少米时,矩形ABCD的面积最大,最大面积为多少?

答案：
(1)由题意，得$3x+20+GC=100$，
∴$GC=(80-3x)m$.
∵$BC=BG+GC=10+80-3x=90-3x$，$10＜BC\leqslant30$，
∴$20\leqslant x＜\frac{80}{3}$.
$S_{矩形DCHG}=(80-3x)x=125$，解得$x_{1}=25$，$x_{2}=\frac{5}{3}$（舍去）.
答：CD的长为25m.
(2)设矩形ABCD的面积为S，则$S=x(90-3x)=-3x^{2}+90x=-3(x-15)^{2}+675$.
∵$-3＜0$，
∴抛物线开口向下，且$20\leqslant x＜\frac{80}{3}$.
∴当$x＞15$时，S随x的增大而减小.
∴当$x=20$时，S取得最大值，为$-3×(20-15)^{2}+675=600$.
答：当CD的长为20m时，矩形ABCD的面积最大，最大面积为$600m^{2}$.