《2025年一阅优品作业本九年级数学全一册人教版》

7. 一个不透明的盒子里装有黑、白两种球(只有颜色不同)共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中.不断重复上述过程,得到"摸到白球"的频率的折线统计图如下.

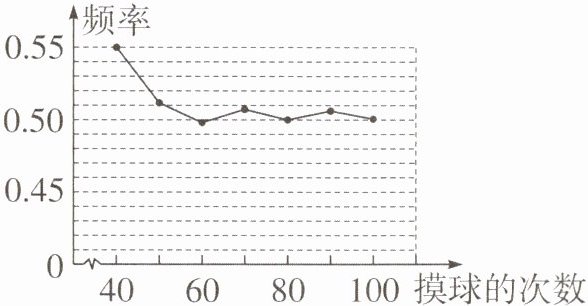
(1) 请估计:当摸球次数n很大时,摸到白球的概率将会接近______(精确到0.01).假如你摸一次,你摸到白球的概率为______.
(2) 估算盒子里白、黑两种颜色的球各有多少个.
(3) 在题(2)的条件下,如果要使摸到白球的概率为$\frac{3}{5}$,需要往盒子里再放入多少个白球?

答案： （1）0.50 0.5
（2）40×0.5=20(个),40 - 20=20(个).
答:盒子里白、黑两种颜色的球各有 20 个.
（3）设需要往盒子里再放入 x 个白球.
根据题意,得$\frac{20 + x}{40 + x}=\frac{3}{5}$,解得 x = 10.
经检验,x = 10 是原方程的解.
答:需要往盒子里再放入 10 个白球.

8. 在一次有奖销售活动中,共发行奖券1000张,凡购满100元商品者得奖券一张.这次有奖销售设一等奖1名,奖金500元;二等奖2名,奖金各200元;三等奖10名,奖金各50元;四等奖100名,奖金各10元.
(1) 求奖金总额,并与九五折销售相比,说明哪一种销售方法给消费者让利较多.
(2) 若某人购买了100元的商品,他中一、二、三、四等奖的概率分别是多少?
(3) 若某人购买了100元的商品,他中奖的概率是多少?

答案： （1）九五折销售让利额=100×1000×(1 - 95%)=100000×5%=5000(元).
奖金总额=500+200×2+50×10+10×100=2400(元).
∵5000＞2400,
∴打折销售给消费者让利较多.
（2）中一等奖的概率=1÷1000=$\frac{1}{1000}$.
中二等奖的概率=2÷1000=$\frac{1}{500}$.
中三等奖的概率=10÷1000=$\frac{1}{100}$.
中四等奖的概率=100÷1000=$\frac{1}{10}$.
（3）中奖的概率=(1 + 2 + 10 + 100)÷1000=$\frac{113}{1000}$.

9. 小红和小明在操场做游戏,如图①,他们先在地上画了半径分别为OB= 2m和OA= 3m的同心圆,蒙上眼睛在一定距离外向圈内投掷小石子,若掷中涂色部分,则小红胜;否则小明胜.(未掷中圈内不算)

(1) 你认为游戏公平吗?为什么?
(2) 能否利用上面游戏中用到的"用频率来估算概率"的原理来估算图②矩形ABCD中的不规则图形的面积?其中AB= 2m,BC= 3m.(说明设计方案的实施步骤和如何估算不规则图形的面积)

答案： （1）不公平.
理由:
∵圆环的面积为$3^{2}×π - 2^{2}×π = 5π$,小圆的面积为$4π$,
∴P(小红胜)=$\frac{5π}{9π}=\frac{5}{9}$,P(小明胜)=$\frac{4π}{9π}=\frac{4}{9}$.
∵$\frac{5}{9}＞\frac{4}{9}$,
∴游戏不公平.
（2）能.
蒙上眼睛在一定距离外向矩形内投掷小石子,落在矩形内 m(尽可能多)次,不规则图形内 n 次,则不规则图形的面积为$\frac{n}{m}×2×3=\frac{6n}{m}(m^{2})$.