《2025年一阅优品作业本九年级数学全一册人教版》

一、连半径构造直角三角形
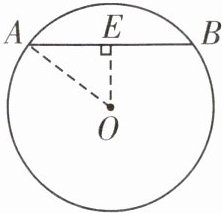
·母题:如图,在$\odot O$中,弦$AB的长为8\ cm$,圆心$O到AB的距离为3\ cm$,求$\odot O$的半径.

答案： 根据题意,得$AE=\frac{1}{2}AB=\frac{1}{2}×8=4(cm)$,$OE=3cm$.
$\therefore OA=\sqrt{AE^{2}+OE^{2}}=\sqrt{4^{2}+3^{2}}=5(cm)$.

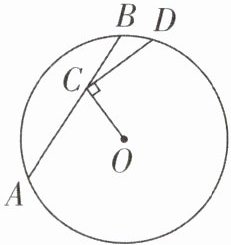
·变式1:如图,在$\odot O$中,弦$AB= 1$,点$C在AB$上移动,连接$OC$,过点$C作CD\perp OC$,交$\odot O于点D$,则$CD$的最大值为______.

答案： $\frac{1}{2}$

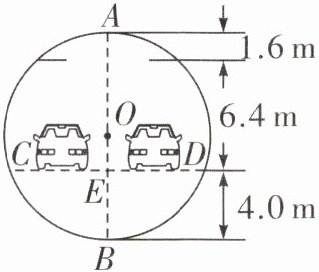
·变式2:下图是一张盾构隧道断面结构图,隧道内部是以$O$为圆心,$AB$为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点$A到顶棚的距离为1.6\ m$,顶棚到路面的距离为$6.4\ m$,点$B到路面的距离为4.0\ m$.请求出路面$CD$的宽.

答案： 连接$OD$.
由题意,得$AB=1.6+6.4+4.0=12.0(m)$.
$\therefore OB=OD=\frac{1}{2}AB=6.0(m)$.
$\because BE=4.0m$,$\therefore OE=OB - BE=2.0(m)$.
在$Rt\triangle OED$中,$DE=\sqrt{OD^{2}-OE^{2}}=4\sqrt{2}(m)$.
$\therefore CD=2DE=8\sqrt{2}(m)$.
$\therefore$路面$CD$的宽为$8\sqrt{2}m$.

·变式3:《九章算术》是中国传统数学的重要著作,奠定了中国传统数学的基本框架.《九章算术》中记载:"今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺(如图①),问径几何?"阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中$BO\perp CD于点A$,要求的是$\odot O$的直径.再次阅读后,发现$AB= $______寸,$CD= $______寸.(1尺$=10$寸)
请你补全题目条件,并帮助小智求出$\odot O$的直径.

答案：
1 10
如图,连接$CO$

$\because BO\perp CD$,$\therefore CA=\frac{1}{2}CD=5(寸)$.
设$CO=OB=x$寸,则$AO=(x - 1)$寸.
在$Rt\triangle CAO$中,$AO^{2}+CA^{2}=CO^{2}$,即$(x - 1)^{2}+5^{2}=x^{2}$,解得$x=13$.
$\therefore \odot O$的直径为26寸.

·母题:$\odot O的半径为13\ cm$,$AB$,$CD是\odot O$的两条弦,$AB// CD$,$AB= 24\ cm$,$CD= 10\ cm$.求$AB和CD$之间的距离.

答案：
①如图,两弦在圆心的不同侧时,已知$CD=10cm$,则$DE=5cm$.

$\because OD=13cm$,$\therefore OE=\sqrt{OD^{2}-DE^{2}}=12(cm)$.
同理可得$OF=5cm$.
$\therefore EF=OE+OF=17(cm)$.
②两弦在圆心的同一侧时,$EF=OE - OF=7(cm)$.
综上所述,$AB$和$CD$之间的距离为17cm或7cm.