《2025年一阅优品作业本九年级数学全一册人教版》

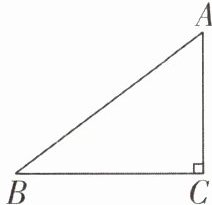
9. 如图,在△ABC中,∠ACB= 90°,AB= 5,BC= 4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A,D之间的距离(不要求尺规作图).

答案： 图略.
∵△ABC绕点C顺时针旋转90°得到△DEC,
∴AC=DC,∠ACD=90°.
∵AC=$\sqrt{AB^2-BC^2}$=3,
∴AD=$\sqrt{AC^2+CD^2}$=$3\sqrt{2}$.

10.【问题解决】
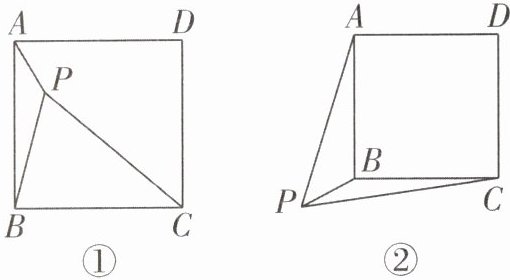
在某节数学课上,老师提出了这样一个问题:如图①,P是正方形ABCD内一点,PA= 1,PB= 2,PC= 3,求∠APB的度数.
小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP',求∠APB的度数.
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP',求∠APB的度数.
(1)请在小明的思路中任选一种,写出完整的解答过程.
【类比探究】
(2)如图②,P是正方形ABCD外一点,PA= 3,PB= 1,PC= $\sqrt{11}$,求∠APB的度数.

答案：

(1)选思路一:如图①，将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP'.
∴∠PBP'=90°,BP'=BP=2,AP'=CP=3.
∴在Rt△PBP'中,∠BPP'=45°,PP'=$2\sqrt{2}$.
∵AP=1,
∴AP²+PP'²=1+8=9.
∵AP'²=$3^2$=9,
∴AP²+PP'²=AP'².
∴△APP'是直角三角形,且∠APP'=90°.
∴∠APB=∠APP'+∠BPP'=90°+45°=135°.
选思路二:方法同思路一.
　　　　 　　
(2)如图②,将△BPC绕点B逆时针旋转90°,得到△BP'A,连接PP'.
∴∠PBP'=90°,BP'=BP=1,AP'=CP=$\sqrt{11}$.
∴在Rt△PBP'中,∠BPP'=45°,PP'=$\sqrt{2}$.
∵AP=3,
∴AP²+PP'²=9+2=11.
∵AP'²=$(\sqrt{11})^2$=11,
∴AP²+PP'²=AP'².
∴△APP'是直角三角形,且∠APP'=90°.
∴∠APB=∠APP'-∠BPP'=90°-45°=45°.