《2025年一阅优品作业本九年级数学全一册人教版》

7. 有1人患了流感,经过两轮传染后共有81人患了流感.设每轮传染中每人传染x人,其中20%的人因自身抵抗力强而未患流感,则根据题意可列方程 ( )

A.$0.2(1+x)^{2}= 81$
B.$(1+0.2x)^{2}= 81$
C.$0.8(1+x)^{2}= 81$
D.$(1+0.8x)^{2}= 81$

答案： D

8. (2023·商洛期末)白云航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有______个飞机场.

答案： 5

9. 小明同学是一位古诗文的爱好者,他在学习了一元二次方程这一章后,改编了苏轼的词《念奴娇·赤壁怀古》:"大江东去,浪淘尽,千古风流人物.而立之年督东吴,早逝英年两位数.十位恰小个位三,个位平方与寿同.哪位学子算得快,多少年华数周瑜?"假设周瑜去世时年龄的十位数字是x,则可列方程______.

答案： $10x+(x+3)=(x+3)^2$

10. 一个两位数的两个数字之和为5,把这个两位数的个位数字与十位数字互换得到一个新的两位数,它与原两位数的积为736,求这个两位数.

答案： 设这个两位数的十位数字为x，个位数字为(5-x).由题意，得(10x+5-x)[10(5-x)+x]=736.整理，得$x^2-5x+6=0$，解得x₁=2，x₂=3.
∴5-x=3或5-x=2.答：这个两位数是23或32.

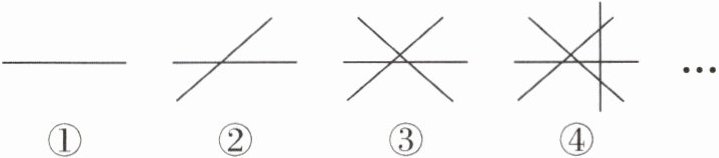
11. 在同一平面上,直线分割平面时,为了使分出的区域尽可能多,则直线之间的交点应尽可能多.如图①,1条直线把平面分成2个区域;如图②,2条直线时要使分成的区域尽可能多,2条直线相交可以把平面分成4个区域;如图③,3条直线时要使分成的区域尽可能多,且避免2条直线相交于一点或平行,三条直线两两相交时最多可以把平面分成7个区域;如图④,4条直线时要分成的区域尽可能多,避免多条直线相交于一点或平行,第4条直线与前3条相交时最多可以把平面分成11个区域……
...
(1)按照此规律,5条直线最多可以把平面分成______个区域.
(2)按照此规律,n条直线最多可以把平面分成______个区域(用含n的式子表示).
(3)最少使用多少条直线,可以把平面分成121个区域?

答案： （1）16 （2）$\frac{n(n+1)}{2}+1$（3）由题
(2)，得$\frac{n(n+1)}{2}+1=121$.整理，得$n^2+n-240=0$，解得x₁=15，x₂=-16(舍去).答：最少使用15条直线，可以把平面分成121个区域.