第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
例 已知直线MN与直线PQ垂直相交于点O,点A在直线PQ上运动,点B在直线MN上运动。

(1)如图1,已知AE,BE分别是∠BAO和∠ABO的平分线,点A,B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小。
(2)如图2,已知AB不平行于CD,AD,BC分别是∠BAP和∠ABM的平分线,DE,CE分别是∠ADC和∠BCD的平分线,点A,B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值。
(3)如图3,延长BA至点G,已知∠BAO,∠OAG的平分线分别与∠BOQ的平分线及反向延长线相交于点E,F,在△AEF中,有一个角是另一个角的3倍,请直接写出∠ABO的度数。
思路点拨
(1)根据直线MN与直线PQ垂直相交于点O可知∠AOB= 90°,由AE,BE分别是∠BAO和∠ABO的平分线得出∠BAE= $\frac{1}{2}$∠BAO,∠ABE= $\frac{1}{2}$∠ABO,由三角形内角和定理即可得出结论。(2)延长AD,BC交于点F,根据直线MN与直线PQ垂直相交于点O可得出∠AOB= 90°,进而得出∠BAO+∠ABO= 90°,故∠BAP+∠ABM= 270°,由AD,BC分别是∠BAP和∠ABM的平分线,可知∠BAD= $\frac{1}{2}$∠BAP,∠ABC= $\frac{1}{2}$∠ABM,由三角形内角和定理可知∠F= 45°,再根据DE,CE分别是∠ADC和∠BCD的平分线可知∠CDE+∠DCE= 112.5°,进而可得出结论。(3)由∠BAO与∠BOQ的平分线相交于点E可知∠EAO= $\frac{1}{2}$∠BAO,∠EOQ= $\frac{1}{2}$∠BOQ,进而得出∠E= ∠EOQ-∠EAO= $\frac{1}{2}$(∠BOQ-∠BAO)= $\frac{1}{2}$∠ABO,由AE,AF分别是∠BAO和∠OAG的平分线可知∠EAF= 90°,在△AEF中,一个角是另一个角的3倍,则需分四种情况进行分类讨论。
解题过程
(1)∠AEB的大小不变。∵直线MN与直线PQ垂直相交于点O,∴∠AOB= 90°。∴∠BAO+∠ABO= 90°。∵AE,BE分别是∠BAO和∠ABO的平分线,∴∠BAE= $\frac{1}{2}$∠BAO,∠ABE= $\frac{1}{2}$∠ABO。∴∠BAE+∠ABE= $\frac{1}{2}$(∠BAO+∠ABO)= 45°。∴∠AEB= 135°。
(2)∠CED的大小不变。如图4,延长AD,BC交于点F。
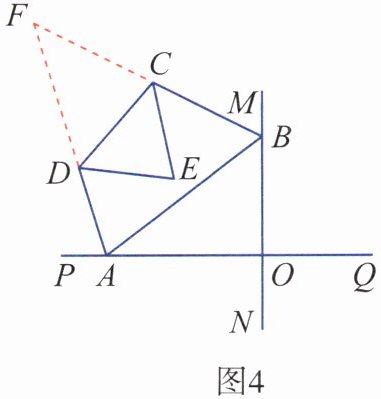
∵直线MN与直线PQ垂直相交于点O,∴∠AOB= 90°。∴∠BAO+∠ABO= 90°。∴∠BAP+∠ABM= 270°。∵AD,BC分别是∠BAP和∠ABM的平分线,∴∠BAD= $\frac{1}{2}$∠BAP,∠ABC= $\frac{1}{2}$∠ABM。∴∠BAD+∠ABC= $\frac{1}{2}$(∠BAP+∠ABM)= 135°。∴∠F= 45°。∴∠FDC+∠FCD= 135°。∴∠CDA+∠DCB= 225°。∵DE,CE分别是∠ADC和∠BCD的平分线,∴∠CDE= $\frac{1}{2}$∠CDA,∠DCE= $\frac{1}{2}$∠DCB。∴∠CDE+∠DCE= $\frac{1}{2}$(∠CDA+∠DCB)= 112.5°。∴∠CED= 67.5°。
(3)∵∠BAO与∠BOQ的平分线相交于点E,∴∠EAO= $\frac{1}{2}$∠BAO,∠EOQ= $\frac{1}{2}$∠BOQ。∴∠E= ∠EOQ-∠EAO= $\frac{1}{2}$(∠BOQ-∠BAO)= $\frac{1}{2}$∠ABO。∵AE,AF分别是∠BAO和∠OAG的平分线,∴∠EAF= 90°。在△AEF中,有一个角是另一个角的3倍,则:①当∠EAF= 3∠E时,∠E= 30°,此时∠ABO= 60°;②当∠EAF= 3∠F时,∠E= 60°,此时∠ABO= 120°(不合题意,舍去);③当∠F= 3∠E时,∠E= 22.5°,此时∠ABO= 45°;④当∠E= 3∠F时,∠E= 67.5°,此时∠ABO= 135°(不合题意,舍去)。∴∠ABO的度数为60°或45°。
方法归纳
本题考查了三角形内角和定理,解题思路是将角度的计算转化为三角形中内角之间的关系,同时结合角平分线的定义研究角之间的数量关系。熟知三角形内角和是180°是解答本题的关键。
易错误区
本题图形比较复杂,要认真研究图形,注意各个小题之间图形的变化,题(3)还要根据图形的变化进行分类讨论。

(1)如图1,已知AE,BE分别是∠BAO和∠ABO的平分线,点A,B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小。
(2)如图2,已知AB不平行于CD,AD,BC分别是∠BAP和∠ABM的平分线,DE,CE分别是∠ADC和∠BCD的平分线,点A,B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值。
(3)如图3,延长BA至点G,已知∠BAO,∠OAG的平分线分别与∠BOQ的平分线及反向延长线相交于点E,F,在△AEF中,有一个角是另一个角的3倍,请直接写出∠ABO的度数。
思路点拨
(1)根据直线MN与直线PQ垂直相交于点O可知∠AOB= 90°,由AE,BE分别是∠BAO和∠ABO的平分线得出∠BAE= $\frac{1}{2}$∠BAO,∠ABE= $\frac{1}{2}$∠ABO,由三角形内角和定理即可得出结论。(2)延长AD,BC交于点F,根据直线MN与直线PQ垂直相交于点O可得出∠AOB= 90°,进而得出∠BAO+∠ABO= 90°,故∠BAP+∠ABM= 270°,由AD,BC分别是∠BAP和∠ABM的平分线,可知∠BAD= $\frac{1}{2}$∠BAP,∠ABC= $\frac{1}{2}$∠ABM,由三角形内角和定理可知∠F= 45°,再根据DE,CE分别是∠ADC和∠BCD的平分线可知∠CDE+∠DCE= 112.5°,进而可得出结论。(3)由∠BAO与∠BOQ的平分线相交于点E可知∠EAO= $\frac{1}{2}$∠BAO,∠EOQ= $\frac{1}{2}$∠BOQ,进而得出∠E= ∠EOQ-∠EAO= $\frac{1}{2}$(∠BOQ-∠BAO)= $\frac{1}{2}$∠ABO,由AE,AF分别是∠BAO和∠OAG的平分线可知∠EAF= 90°,在△AEF中,一个角是另一个角的3倍,则需分四种情况进行分类讨论。
解题过程
(1)∠AEB的大小不变。∵直线MN与直线PQ垂直相交于点O,∴∠AOB= 90°。∴∠BAO+∠ABO= 90°。∵AE,BE分别是∠BAO和∠ABO的平分线,∴∠BAE= $\frac{1}{2}$∠BAO,∠ABE= $\frac{1}{2}$∠ABO。∴∠BAE+∠ABE= $\frac{1}{2}$(∠BAO+∠ABO)= 45°。∴∠AEB= 135°。
(2)∠CED的大小不变。如图4,延长AD,BC交于点F。

∵直线MN与直线PQ垂直相交于点O,∴∠AOB= 90°。∴∠BAO+∠ABO= 90°。∴∠BAP+∠ABM= 270°。∵AD,BC分别是∠BAP和∠ABM的平分线,∴∠BAD= $\frac{1}{2}$∠BAP,∠ABC= $\frac{1}{2}$∠ABM。∴∠BAD+∠ABC= $\frac{1}{2}$(∠BAP+∠ABM)= 135°。∴∠F= 45°。∴∠FDC+∠FCD= 135°。∴∠CDA+∠DCB= 225°。∵DE,CE分别是∠ADC和∠BCD的平分线,∴∠CDE= $\frac{1}{2}$∠CDA,∠DCE= $\frac{1}{2}$∠DCB。∴∠CDE+∠DCE= $\frac{1}{2}$(∠CDA+∠DCB)= 112.5°。∴∠CED= 67.5°。
(3)∵∠BAO与∠BOQ的平分线相交于点E,∴∠EAO= $\frac{1}{2}$∠BAO,∠EOQ= $\frac{1}{2}$∠BOQ。∴∠E= ∠EOQ-∠EAO= $\frac{1}{2}$(∠BOQ-∠BAO)= $\frac{1}{2}$∠ABO。∵AE,AF分别是∠BAO和∠OAG的平分线,∴∠EAF= 90°。在△AEF中,有一个角是另一个角的3倍,则:①当∠EAF= 3∠E时,∠E= 30°,此时∠ABO= 60°;②当∠EAF= 3∠F时,∠E= 60°,此时∠ABO= 120°(不合题意,舍去);③当∠F= 3∠E时,∠E= 22.5°,此时∠ABO= 45°;④当∠E= 3∠F时,∠E= 67.5°,此时∠ABO= 135°(不合题意,舍去)。∴∠ABO的度数为60°或45°。
方法归纳
本题考查了三角形内角和定理,解题思路是将角度的计算转化为三角形中内角之间的关系,同时结合角平分线的定义研究角之间的数量关系。熟知三角形内角和是180°是解答本题的关键。
易错误区
本题图形比较复杂,要认真研究图形,注意各个小题之间图形的变化,题(3)还要根据图形的变化进行分类讨论。
答案:
【解析】:
(1)题目考查了三角形内角和定理及角平分线的性质。
根据直线$MN$与直线$PQ$垂直相交于点$O$,可得$\angle AOB = 90^\circ$。
因为$AE$、$BE$分别是$\angle BAO$和$\angle ABO$的平分线,所以$\angle BAE=\frac{1}{2}\angle BAO$,$\angle ABE=\frac{1}{2}\angle ABO$。
由三角形内角和定理,$\angle AEB=180^\circ-(\angle BAE + \angle ABE)=180^\circ-\frac{1}{2}(\angle BAO + \angle ABO)=135^\circ$。
因此,$\angle AEB$的大小不发生变化,为$135^\circ$。
(2)题目考查了三角形内角和定理及外角性质,以及角平分线的性质。
延长$AD$、$BC$交于点$F$。
由直线$MN$与直线$PQ$垂直相交于点$O$,得$\angle AOB = 90^\circ$,则$\angle BAO + \angle ABO = 90^\circ$,所以$\angle BAP + \angle ABM = 270^\circ$。
因为$AD$、$BC$分别是$\angle BAP$和$\angle ABM$的平分线,所以$\angle BAD=\frac{1}{2}\angle BAP$,$\angle ABC=\frac{1}{2}\angle ABM$。
从而$\angle BAD + \angle ABC =\frac{1}{2}(\angle BAP + \angle ABM)=135^\circ$。
在$\triangle ABF$中,$\angle F = 45^\circ$,所以$\angle FDC + \angle FCD = 135^\circ$,则$\angle CDA + \angle DCB = 225^\circ$。
又因为$DE$、$CE$分别是$\angle ADC$和$\angle BCD$的平分线,所以$\angle CDE=\frac{1}{2}\angle CDA$,$\angle DCE=\frac{1}{2}\angle DCB$。
因此,$\angle CDE + \angle DCE =\frac{1}{2}(\angle CDA + \angle DCB)=112.5^\circ$。
在$\triangle CDE$中,$\angle CED = 67.5^\circ$。
所以,$\angle CED$的大小不发生变化,为$67.5^\circ$。
(3)题目考查了三角形内角和定理,角平分线的性质,以及分类讨论的数学思想。
由$\angle BAO$与$\angle BOQ$的平分线相交于点$E$,可得$\angle EAO=\frac{1}{2}\angle BAO$,$\angle EOQ=\frac{1}{2}\angle BOQ$。
根据三角形外角性质,$\angle E=\angle EOQ - \angle EAO=\frac{1}{2}(\angle BOQ - \angle BAO)=\frac{1}{2}\angle ABO$。
因为$AE$、$AF$分别是$\angle BAO$和$\angle OAG$的平分线,所以$\angle EAF = 90^\circ$。
在$\triangle AEF$中,一个角是另一个角的$3$倍,需分四种情况进行讨论:
当$\angle EAF = 3\angle E$时,$\angle E = 30^\circ$,此时$\angle ABO = 60^\circ$;
当$\angle EAF = 3\angle F$时,$\angle E = 60^\circ$,此时$\angle ABO = 120^\circ$(不合题意,舍去);
当$\angle F = 3\angle E$时,$\angle E = 22.5^\circ$,此时$\angle ABO = 45^\circ$;
当$\angle E = 3\angle F$时,$\angle E = 67.5^\circ$,此时$\angle ABO = 135^\circ$(不合题意,舍去)。
综上,$\angle ABO$的度数为$60^\circ$或$45^\circ$。
【答案】:
(1) $\angle AEB$的大小不变,$\angle AEB = 135^\circ$;
(2) $\angle CED$的大小不变,$\angle CED = 67.5^\circ$;
(3) $\angle ABO$的度数为$60^\circ$或$45^\circ$。
(1)题目考查了三角形内角和定理及角平分线的性质。
根据直线$MN$与直线$PQ$垂直相交于点$O$,可得$\angle AOB = 90^\circ$。
因为$AE$、$BE$分别是$\angle BAO$和$\angle ABO$的平分线,所以$\angle BAE=\frac{1}{2}\angle BAO$,$\angle ABE=\frac{1}{2}\angle ABO$。
由三角形内角和定理,$\angle AEB=180^\circ-(\angle BAE + \angle ABE)=180^\circ-\frac{1}{2}(\angle BAO + \angle ABO)=135^\circ$。
因此,$\angle AEB$的大小不发生变化,为$135^\circ$。
(2)题目考查了三角形内角和定理及外角性质,以及角平分线的性质。
延长$AD$、$BC$交于点$F$。
由直线$MN$与直线$PQ$垂直相交于点$O$,得$\angle AOB = 90^\circ$,则$\angle BAO + \angle ABO = 90^\circ$,所以$\angle BAP + \angle ABM = 270^\circ$。
因为$AD$、$BC$分别是$\angle BAP$和$\angle ABM$的平分线,所以$\angle BAD=\frac{1}{2}\angle BAP$,$\angle ABC=\frac{1}{2}\angle ABM$。
从而$\angle BAD + \angle ABC =\frac{1}{2}(\angle BAP + \angle ABM)=135^\circ$。
在$\triangle ABF$中,$\angle F = 45^\circ$,所以$\angle FDC + \angle FCD = 135^\circ$,则$\angle CDA + \angle DCB = 225^\circ$。
又因为$DE$、$CE$分别是$\angle ADC$和$\angle BCD$的平分线,所以$\angle CDE=\frac{1}{2}\angle CDA$,$\angle DCE=\frac{1}{2}\angle DCB$。
因此,$\angle CDE + \angle DCE =\frac{1}{2}(\angle CDA + \angle DCB)=112.5^\circ$。
在$\triangle CDE$中,$\angle CED = 67.5^\circ$。
所以,$\angle CED$的大小不发生变化,为$67.5^\circ$。
(3)题目考查了三角形内角和定理,角平分线的性质,以及分类讨论的数学思想。
由$\angle BAO$与$\angle BOQ$的平分线相交于点$E$,可得$\angle EAO=\frac{1}{2}\angle BAO$,$\angle EOQ=\frac{1}{2}\angle BOQ$。
根据三角形外角性质,$\angle E=\angle EOQ - \angle EAO=\frac{1}{2}(\angle BOQ - \angle BAO)=\frac{1}{2}\angle ABO$。
因为$AE$、$AF$分别是$\angle BAO$和$\angle OAG$的平分线,所以$\angle EAF = 90^\circ$。
在$\triangle AEF$中,一个角是另一个角的$3$倍,需分四种情况进行讨论:
当$\angle EAF = 3\angle E$时,$\angle E = 30^\circ$,此时$\angle ABO = 60^\circ$;
当$\angle EAF = 3\angle F$时,$\angle E = 60^\circ$,此时$\angle ABO = 120^\circ$(不合题意,舍去);
当$\angle F = 3\angle E$时,$\angle E = 22.5^\circ$,此时$\angle ABO = 45^\circ$;
当$\angle E = 3\angle F$时,$\angle E = 67.5^\circ$,此时$\angle ABO = 135^\circ$(不合题意,舍去)。
综上,$\angle ABO$的度数为$60^\circ$或$45^\circ$。
【答案】:
(1) $\angle AEB$的大小不变,$\angle AEB = 135^\circ$;
(2) $\angle CED$的大小不变,$\angle CED = 67.5^\circ$;
(3) $\angle ABO$的度数为$60^\circ$或$45^\circ$。
查看更多完整答案,请扫码查看


