《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

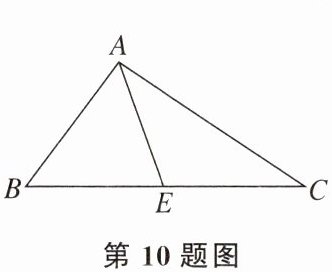
10. 如图,在△ABC中,E是BC的中点,AB= 7,AC= 10,△ACE的周长是25,则△ABE的周长是22。

答案： 22

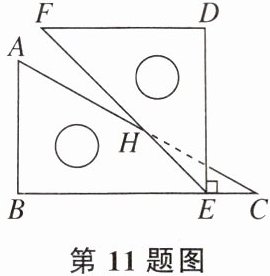
11. 把一副三角板按如图所示的方式摆放,$∠A= 60°,∠F= 45°,DE⊥BC,$则∠CHE的度数为15°。

答案： 15°

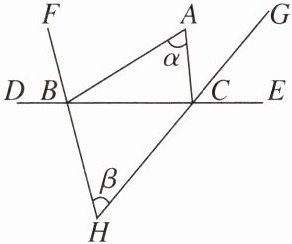
12. 如图,∠ABD和∠ACE是△ABC的外角,BF和CG分别是∠ABD和∠ACE的平分线,延长FB和GC交于点H。设∠A= α,∠H= β,则α与β之间的数量关系为α+2β=180°。

答案： α+2β=180°【解析】因为BF和CG分别是∠ABD和∠ACE的平分线，所以设∠ABF=∠DBF=θ，∠ACG=∠ECG=φ，则∠ABD=2θ，∠CBH=∠DBF=θ，∠ACE=2φ，∠BCH=∠ECG=φ，所以∠ABC=180°-∠ABD=180°-2θ，∠ACB=180°-∠ACE=180°-2φ。在△ABC中，∠A+∠ABC+∠ACB=180°，所以α+180°-2θ+180°-2φ=180°。整理得，θ+φ=90°+$\frac{1}{2}$α，在△HBC中，∠H+∠CBH+∠BCH=180°，所以β+θ+φ=180°，所以β+90°+$\frac{1}{2}$α=180°，整理得，α+2β=180°。所以α与β之间的数量关系为α+2β=180°。

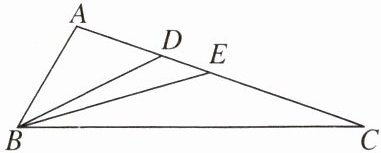
13. (12分)如图,BD是△ABC的角平分线,BE是△ABC的AC边上的中线。
(1)若△ABE的周长为13,BE= 6,CE= 4,求AB的长。
(2)若$∠A= 92^\circ,∠CBD= 34^\circ,$求∠C的度数。

答案：
(1)3；
(2)20°【解析】
(1)因为BE是△ABC的AC边上的中线，所以AE=CE。因为CE=4，所以AE=4。因为△ABE的周长为13，所以AB+AE+BE=13，所以AB+BE=9。因为BE=6，所以AB=3。
(2)因为BD是△ABC的角平分线，∠CBD=34°，所以∠CBA=2∠CBD=68°。因为∠A=92°，所以∠C=180°-∠A-∠CBA=180°-92°-68°=20°。

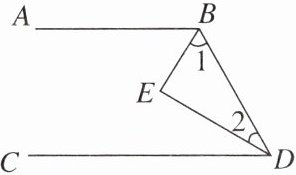
14. (12分)如图,①AB//CD,②BE平分∠ABD,$③∠1+∠2= 90^\circ,$④DE平分∠BDC。
(1)请以其中三个为条件,第四个为结论,写出一个命题。
(2)判断这个命题是否为真命题,并说明理由。

答案：
(1)答案不唯一，如：如果BE平分∠ABD，DE平分∠BDC，∠1+∠2=90°，那么AB//CD。
(2)这个命题是真命题，理由如下：因为BE平分∠ABD，所以∠1=$\frac{1}{2}$∠ABD。因为DE平分∠BDC，所以∠2=$\frac{1}{2}$∠BDC。因为∠1+∠2=90°，所以∠ABD+∠BDC=180°，所以AB//CD。

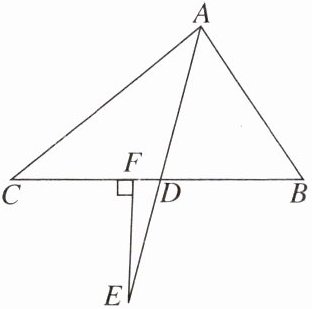
15. (12分)如图,在△ABC中,∠B＞∠C,AD平分∠BAC,点E在AD的延长线上,过点E作EF⊥BC于点F,设∠B= α,∠C= β。
(1)当$α=80^\circ,β=30^\circ$时,求∠E的度数。
(2)试问∠E与∠B,∠C之间存在着怎样的数量关系？试用α,β表示∠E,并说明理由。

答案：
(1)25°；
(2)∠E=$\frac{1}{2}$(α-β)【解析】
(1)因为∠B=80°，∠C=30°，所以∠BAC=180°-80°-30°=70°。因为AD平分∠BAC，所以∠BAD=$\frac{1}{2}$∠BAC=35°，所以∠EDF=∠ADB=180°-35°-80°=65°。因为EF⊥BC，所以∠EFD=90°，所以∠E=90°-65°=25°。
(2)因为∠EDF=180°-∠ADC=180°-[180°-(∠C+∠CAD)]=∠C+∠CAD，∠CAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-α-β)，所以∠EDF=∠C+90°-$\frac{1}{2}$α-$\frac{1}{2}$β=90°-$\frac{1}{2}$(α-β)。因为∠EFD=90°，所以∠E=$\frac{1}{2}$(α-β)。