《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

9. 判断下列长度的三条线段中,哪些能组成三角形,哪些不能组成三角形,并说明理由。
(1)$a= 2\ cm$,$b= 5\ cm$,$c= 7.5\ cm$。
(2)$a= b= 100\ cm$,$c= 1\ cm$。
(3)$a= (k+1)\ cm$,$b= (k+2)\ cm$,$c= (2k+2)\ cm(k＞0)$。

答案： 解:
(1)不能组成三角形。理由:因为最长线段c = 7.5cm，a + b = 2 + 5 = 7(cm)，所以a + b＜c，所以线段a，b，c不能组成三角形。
(2)能组成三角形。理由:因为a + c = 100 + 1 = 101(cm)，a + c＞b，所以线段a，b，c能组成三角形。
(3)能组成三角形。理由:因为最长线段c = (2k + 2)cm，a + b = (2k + 3)cm，所以a + b＞c，所以线段a，b，c能组成三角形。

10. 如图,一只手握住了一个三角形的一部分,则这个三角形是 (D)

A.钝角三角形
B.直角三角形
C.锐角三角形
D.钝角三角形或直角三角形或锐角三角形

答案： D

11. 已知三角形的两边$a= 3$,$b= 7$,第三边是$c$。
(1)第三边$c$的长度的取值范围是4＜c＜10。
(2)若第三边$c$的长为偶数,则$c$的值为6或8。
(3)若$a＜b＜c$,则$c$的取值范围是7＜c＜10。

答案：
(1)4＜c＜10
(2)6或8
(3)7＜c＜10

12. 某建材市场上的一种钢管的长度规格及相应价格如下表：

学校要制作一个三角形支架的宣传牌,已经购买两根长度分别为 2 m 和 5 m 的钢管,还需要购买一根。
(1)有哪几种规格的钢管可供选择？
(2)若要求做成的三角形支架的周长为偶数,则要做成三角形支架,一共需要花多少钱购买钢管？

答案： 解:
(1)设第三根钢管的长度为x m，则5 - 2＜x＜5 + 2，即3＜x＜7，所以有长度为4m，5m，6m的钢管可供选择。
(2)因为三角形支架的周长为偶数，所以三边长分别为2m，5m，5m，则花的钱数为15×1 + 30×2 = 75(元)。
答:要做成三角形支架，一共需要花75元购买钢管。

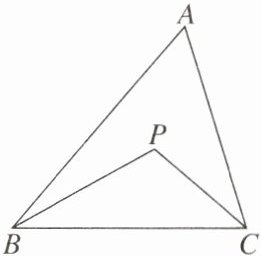
13. 如图,P 为$\triangle ABC$内任意一点,试说明$AB+AC＞PB+PC$。

答案： 解:延长BP交AC于点D，如图。
在△ABD中，PB + PD＜AB + AD，①
在△PCD中，PC＜PD + CD，②
①+②得，PB + PD + PC＜AB + AD + PD + CD，即PB + PC＜AB + AC，即AB + AC＞PB + PC。