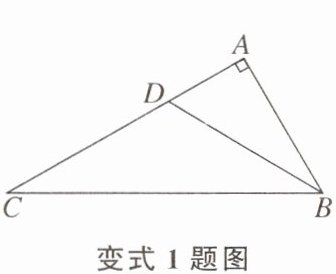
【变式 1】如图,在 Rt△ABC 中,∠A= 90°,∠ABC 的平分线 BD 交 AC 于点 D。若 AD= 2,则点 D 到 BC 的距离为
(
A.1
$B.\sqrt{3}$
$C.\sqrt{5}$
D.2
(
D
)
A.1
$B.\sqrt{3}$
$C.\sqrt{5}$
D.2
答案:
D
【变式 2】如图,△ABC 的面积为$ 10 cm^2,BP $平分∠ABC,过点 A 作 AP⊥BP 于点 P。则△PBC 的面积为_________$cm^2。$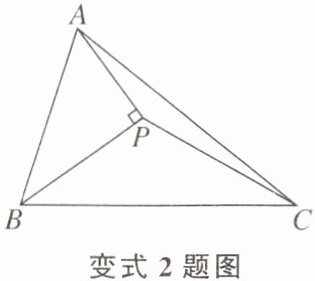

答案:
5【解析】延长 AP 交 BC 于 E,如图。 因为 BP 平分∠ABC,所以∠ABP=∠EBP。因为 AP⊥BP,所以∠APB=∠EPB=90°。在△ABP 和△EBP 中,$\begin{cases}∠ABP=∠EBP, \\ BP=BP, \\ ∠APB=∠EPB,\end{cases}$所以△ABP≌△EBP(ASA),所以 AP=PE,所以 $S_{\triangle ABP}=S_{\triangle EBP}$,$S_{\triangle ACP}=S_{\triangle ECP}$,所以 $S_{\triangle PBC}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}×10=5(cm^2)$。
因为 BP 平分∠ABC,所以∠ABP=∠EBP。因为 AP⊥BP,所以∠APB=∠EPB=90°。在△ABP 和△EBP 中,$\begin{cases}∠ABP=∠EBP, \\ BP=BP, \\ ∠APB=∠EPB,\end{cases}$所以△ABP≌△EBP(ASA),所以 AP=PE,所以 $S_{\triangle ABP}=S_{\triangle EBP}$,$S_{\triangle ACP}=S_{\triangle ECP}$,所以 $S_{\triangle PBC}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}×10=5(cm^2)$。
5【解析】延长 AP 交 BC 于 E,如图。
 因为 BP 平分∠ABC,所以∠ABP=∠EBP。因为 AP⊥BP,所以∠APB=∠EPB=90°。在△ABP 和△EBP 中,$\begin{cases}∠ABP=∠EBP, \\ BP=BP, \\ ∠APB=∠EPB,\end{cases}$所以△ABP≌△EBP(ASA),所以 AP=PE,所以 $S_{\triangle ABP}=S_{\triangle EBP}$,$S_{\triangle ACP}=S_{\triangle ECP}$,所以 $S_{\triangle PBC}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}×10=5(cm^2)$。
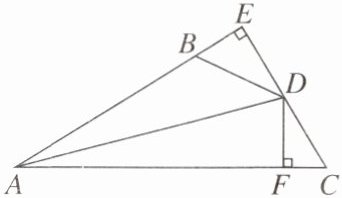
因为 BP 平分∠ABC,所以∠ABP=∠EBP。因为 AP⊥BP,所以∠APB=∠EPB=90°。在△ABP 和△EBP 中,$\begin{cases}∠ABP=∠EBP, \\ BP=BP, \\ ∠APB=∠EPB,\end{cases}$所以△ABP≌△EBP(ASA),所以 AP=PE,所以 $S_{\triangle ABP}=S_{\triangle EBP}$,$S_{\triangle ACP}=S_{\triangle ECP}$,所以 $S_{\triangle PBC}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}×10=5(cm^2)$。 【变式 3】如图,DE⊥AB 交 AB 的延长线于点 E,DF⊥AC 于点 F,若 BD= CD,BE= CF。求证:AD 平分∠BAC。

答案:
证明:因为 DE⊥AE,DF⊥AC,所以∠E=∠DFC=90°。在 Rt△BDE 和 Rt△CDF 中,因为$\begin{cases}BD=CD, \\ BE=CF,\end{cases}$所以 Rt△BDE≌Rt△CDF(HL),所以 DE=DF,所以 AD 平分∠BAC。
【例 3】如图,有一张三角形纸片 ABC,∠C= 90°,AC= 8 cm,BC= 6 cm,现将纸片折叠,使点 A 与点 B 重合,求折痕的长度。


答案:
解:如图,折痕为 DE。 因为在 Rt△ABC 中,∠C=90°,AC=8 cm,BC=6 cm,所以根据勾股定理得,AB= $\sqrt{AC^2+BC^2}$=10 cm。设 CE=x cm,由折叠的性质得BD=AD=5 cm,BE=AE=(8-x)cm。在 Rt△BCE 中,根据勾股定理可知,$BC^2+CE^2$=$BE^2$,即$6^2+x^2=(8-x)^2$,解得 x= $\frac{7}{4}$,故折痕长 DE= $\sqrt{AE^2-AD^2}=\frac{15}{4}$cm。
因为在 Rt△ABC 中,∠C=90°,AC=8 cm,BC=6 cm,所以根据勾股定理得,AB= $\sqrt{AC^2+BC^2}$=10 cm。设 CE=x cm,由折叠的性质得BD=AD=5 cm,BE=AE=(8-x)cm。在 Rt△BCE 中,根据勾股定理可知,$BC^2+CE^2$=$BE^2$,即$6^2+x^2=(8-x)^2$,解得 x= $\frac{7}{4}$,故折痕长 DE= $\sqrt{AE^2-AD^2}=\frac{15}{4}$cm。
解:如图,折痕为 DE。
 因为在 Rt△ABC 中,∠C=90°,AC=8 cm,BC=6 cm,所以根据勾股定理得,AB= $\sqrt{AC^2+BC^2}$=10 cm。设 CE=x cm,由折叠的性质得BD=AD=5 cm,BE=AE=(8-x)cm。在 Rt△BCE 中,根据勾股定理可知,$BC^2+CE^2$=$BE^2$,即$6^2+x^2=(8-x)^2$,解得 x= $\frac{7}{4}$,故折痕长 DE= $\sqrt{AE^2-AD^2}=\frac{15}{4}$cm。
因为在 Rt△ABC 中,∠C=90°,AC=8 cm,BC=6 cm,所以根据勾股定理得,AB= $\sqrt{AC^2+BC^2}$=10 cm。设 CE=x cm,由折叠的性质得BD=AD=5 cm,BE=AE=(8-x)cm。在 Rt△BCE 中,根据勾股定理可知,$BC^2+CE^2$=$BE^2$,即$6^2+x^2=(8-x)^2$,解得 x= $\frac{7}{4}$,故折痕长 DE= $\sqrt{AE^2-AD^2}=\frac{15}{4}$cm。 【变式 1】如图,有一张直角三角形纸片,∠ACB= 90°,AB= 5 cm,AC= 3 cm,现将△ABC 折叠,使边 AC 与 AB 重合,点 C 的对应点为点 D,折痕为 AE,则 CE 的长为(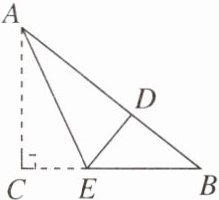
A.1 cm
B.2 cm
$C.\frac{3}{2} cm$
$D.\frac{5}{2} cm$
C
)
A.1 cm
B.2 cm
$C.\frac{3}{2} cm$
$D.\frac{5}{2} cm$
答案:
C
【变式 2】小明将三角形纸片 ABC(AB>AC)沿过点 A 的直线折叠,使得 AC 落在 AB 边上,折痕为 AD,展开纸片(如图 1);再次折叠该三角形纸片,使点 A 和点 D 重合,折痕为 EF,展平纸片后得到△AEF(如图 2)。小明认为△AEF 是等腰三角形,你同意他的说法吗?请你说明理由。
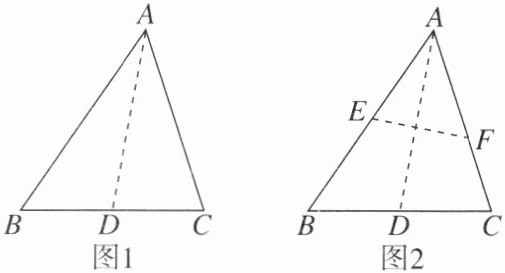

答案:
解:同意。理由:设 AD 与 EF 交于点 G。由第一次折叠知 AD 平分∠BAC,所以∠BAD=∠CAD。由第二次折叠知,∠AGE=∠DGE。又因为∠AGE+∠DGE=180°,所以∠AGE=∠DGE=90°,所以∠AGE=∠AGF=90°,所以∠AEF=∠AFE,所以 AE=AF,即△AEF 为等腰三角形。
查看更多完整答案,请扫码查看


