《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

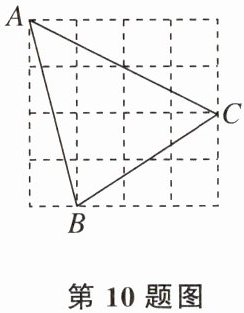
10. 如图,在4×4的网格中,每个小正方形的边长均为1,则点B到直线AC的距离为 (B)

A.$\frac{7\sqrt{10}}{5}$
B.$\frac{7\sqrt{5}}{5}$
C.$\frac{5\sqrt{5}}{5}$
D.$\frac{3\sqrt{5}}{10}$

答案： B

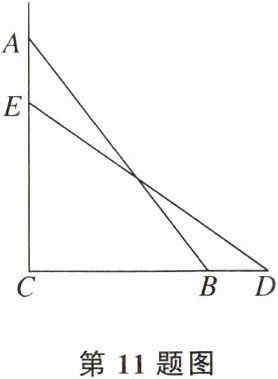
11. 如图,一个梯子AB长2米,顶端A靠在墙AC上,这时梯子下端B与墙角C的距离为1.2米,梯子滑动后停在DE的位置上,测得BD的长为0.4米,则梯子顶端A下滑了 (A)

A.0.4米
B.0.5米
C.0.6米
D.0.7米

答案： A

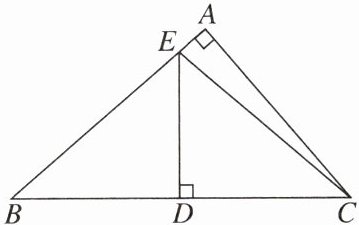
12. 如图,在Rt△ABC中,已知∠A＝90°,D是斜边BC的中点,DE⊥BC交AB于点E,连结CE。
(1)求证：$BE^2 - AE^2 = AC^2$。
(2)若AC＝6,BD＝5,求AE的长。

答案： 解:
(1)证明:因为DE⊥BC，D是斜边BC的中点，所以DE是线段BC的垂直平分线，所以BE=CE。在Rt△ACE中，由勾股定理得，$CE^{2}=AC^{2}+AE^{2}$，所以$BE^{2}=AC^{2}+AE^{2}$，所以$BE^{2}-AE^{2}=AC^{2}$。
(2)因为BD=5，D是斜边BC的中点，所以BC=2BD=10，在Rt△ABC中，由勾股定理得，$AB=\sqrt{BC^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}}=8$，所以AB=BE+AE=8。设AE=x，则BE=CE=8-x，在Rt△ACE中，由勾股定理得，$CE^{2}=AC^{2}+AE^{2}$，即$(8-x)^{2}=6^{2}+x^{2}$，解得$x=\frac{7}{4}$，所以$AE=\frac{7}{4}$，即AE的长为$\frac{7}{4}$。

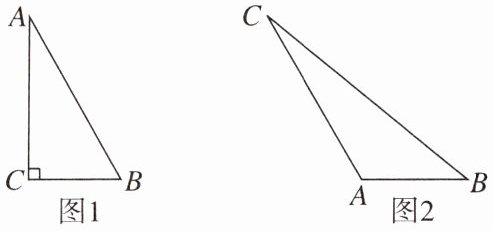
13. (1)如图1,在Rt△ABC中,∠C＝90°,BC＝1,AC＝2,求AB的长。
(2)如图2,在△ABC中,AB＝2,AC＝4,∠A＝120°,求BC的长。
]

答案： 解:
(1)在Rt△ABC中，∠C=90°，所以$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$。
(2)作CD⊥AB交BA的延长线于点D，取AC的中点E，连结DE(图略)。因为∠BAC=120°，所以∠DAC=60°。又因为E为AC的中点，所以$DE=EA=\frac{1}{2}AC$，所以△ADE是等边三角形，所以$AD=\frac{1}{2}AC=2$，所以$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{4^{2}-2^{2}}=\sqrt{12}$，BD=AD+AB=4。在Rt△CDB中，$BC=\sqrt{CD^{2}+BD^{2}}=\sqrt{28}$。