【例3】如图,在△ABC和△DBC中,∠ACB= ∠DBC= 90°,E是BC的中点,DE⊥AB,垂足为点F,且AB= ED。
(1)求证:BD= CB。
(2)若BD= 8cm,求AC的长。
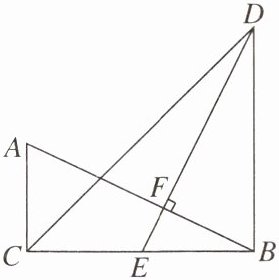
(1)求证:BD= CB。
(2)若BD= 8cm,求AC的长。

答案:
(1)证明:因为∠DBC=90°,所以∠ABC+∠DBF=90°。因为DE⊥AB,所以∠EDB+∠DBF=90°,所以∠ABC=∠EDB。在△EBD和△ACB中,因为∠EBD=∠ACB,∠EDB=∠ABC,ED=AB,所以△EBD≌△ACB(AAS),所以BD=CB。
(2)由
(1)可知△EBD≌△ACB,所以EB=AC。因为E是BC的中点,所以EB=1/2BC。又因为BD=CB,所以EB=1/2BD=1/2×8=4(cm),所以AC=4 cm。
(1)证明:因为∠DBC=90°,所以∠ABC+∠DBF=90°。因为DE⊥AB,所以∠EDB+∠DBF=90°,所以∠ABC=∠EDB。在△EBD和△ACB中,因为∠EBD=∠ACB,∠EDB=∠ABC,ED=AB,所以△EBD≌△ACB(AAS),所以BD=CB。
(2)由
(1)可知△EBD≌△ACB,所以EB=AC。因为E是BC的中点,所以EB=1/2BC。又因为BD=CB,所以EB=1/2BD=1/2×8=4(cm),所以AC=4 cm。
【变式1】如图,已知∠ABC= ∠DCB,添加以下条件,不能判定△ABC≌△DCB的是(
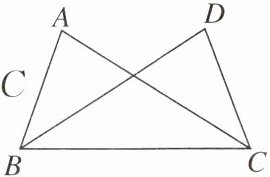
A.∠A= ∠D
B.∠ACB= ∠DBC
C.AC= DB
D.AB= DC
C
)
A.∠A= ∠D
B.∠ACB= ∠DBC
C.AC= DB
D.AB= DC
答案:
C
【变式2】如图,AB= AC,AD= AE,∠BAC= ∠DAE,点D在BC的延长线上,连结EC。
(1)求证:BD= CE。
(2)当∠BAC= ∠DAE= α时,求∠ECD的度数。
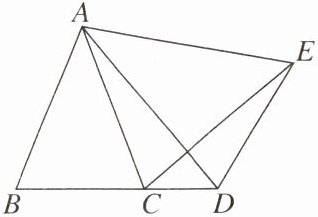
(1)求证:BD= CE。
(2)当∠BAC= ∠DAE= α时,求∠ECD的度数。

答案:
(1)证明:因为∠BAC=∠DAE,所以∠BAC+∠CAD=∠DAE+∠CAD,所以∠BAD=∠CAE。在△ABD和△ACE中,因为AB=AC,∠BAD=∠CAE,AD=AE,所以△ABD≌△ACE(SAS),所以BD=CE。
(2)由
(1)可知,△ABD≌△ACE,所以∠B=∠ACE。因为AB=AC,所以∠B=∠ACE=∠ACB。因为∠BAC+∠B+∠ACB=180°,∠ECD+∠ACE+∠ACB=180°,所以∠ECD=∠BAC=α。
(1)证明:因为∠BAC=∠DAE,所以∠BAC+∠CAD=∠DAE+∠CAD,所以∠BAD=∠CAE。在△ABD和△ACE中,因为AB=AC,∠BAD=∠CAE,AD=AE,所以△ABD≌△ACE(SAS),所以BD=CE。
(2)由
(1)可知,△ABD≌△ACE,所以∠B=∠ACE。因为AB=AC,所以∠B=∠ACE=∠ACB。因为∠BAC+∠B+∠ACB=180°,∠ECD+∠ACE+∠ACB=180°,所以∠ECD=∠BAC=α。
【例4】如图,CD//AB,△ABC的中线AE的延长线与CD相交于点D。
(1)若AE= 3,求DE的长度。
(2)∠DAC的平分线与DC相交于点F,连结EF,若AF= DF,AC= DE,求证:AB= AF+EF。
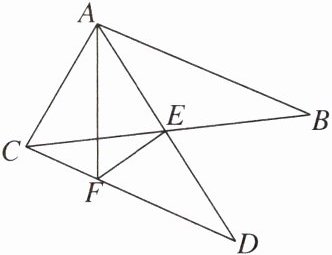
(1)若AE= 3,求DE的长度。
(2)∠DAC的平分线与DC相交于点F,连结EF,若AF= DF,AC= DE,求证:AB= AF+EF。

答案:
(1)因为CD//AB,所以∠B=∠DCE。因为AE是△ABC的中线,所以CE=BE。在△ABE和△DCE中,因为∠B=∠DCE,BE=CE,∠AEB=∠DEC,所以△ABE≌△DCE(ASA),所以AE=DE=3,所以DE的长为3。
(2)证明:因为△ABE≌△DCE,所以AB=CD。因为AF平分∠DAC,所以∠CAF=∠DAF。因为AC=DE,AE=DE,所以AC=AE。在△CAF和△EAF中,因为AC=AE,∠CAF=∠EAF,AF=AF,所以△CAF≌△EAF(SAS),所以CF=EF,所以AB=CD=CF+DF=EF+AF。
(1)因为CD//AB,所以∠B=∠DCE。因为AE是△ABC的中线,所以CE=BE。在△ABE和△DCE中,因为∠B=∠DCE,BE=CE,∠AEB=∠DEC,所以△ABE≌△DCE(ASA),所以AE=DE=3,所以DE的长为3。
(2)证明:因为△ABE≌△DCE,所以AB=CD。因为AF平分∠DAC,所以∠CAF=∠DAF。因为AC=DE,AE=DE,所以AC=AE。在△CAF和△EAF中,因为AC=AE,∠CAF=∠EAF,AF=AF,所以△CAF≌△EAF(SAS),所以CF=EF,所以AB=CD=CF+DF=EF+AF。
【变式】如图,已知△ABC(AB<BC<AC),用尺规在AC上确定一点P,使PB+PC= AC,则下列选项中,一定符合要求的作图痕迹是(
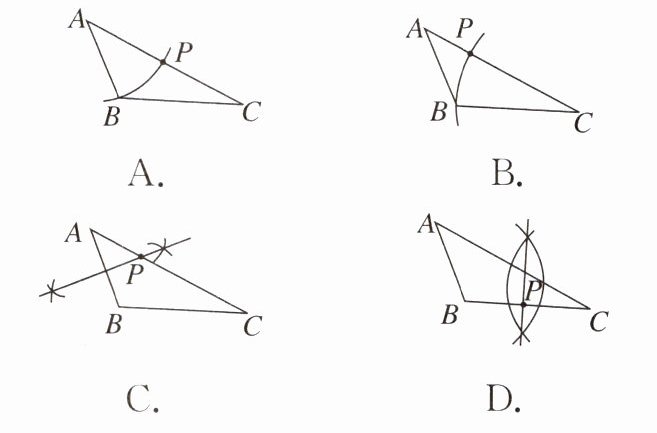
C
)

答案:
C
查看更多完整答案,请扫码查看


