10. 已知点M(x,y),若x-y>0,xy<0,则点M所在的象限是(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
D 【解析】因为x-y>0,xy<0,所以x>0,y<0,所以点M(x,y)所在的象限是第四象限。
11. 已知点A(a-5,2b-1)在y轴上,点B(3a+2,b+3)在x轴上,则点C(a,b)的坐标为(
A.(5,-3)
B.(-5,3)
C.(-5,-3)
D.(5,3)
(5,-3)
)A.(5,-3)
B.(-5,3)
C.(-5,-3)
D.(5,3)
答案:
A 【解析】因为点A(a-5,2b-1)在y轴上,所以a-5=0,解得a=5。因为点B(3a+2,b+3)在x轴上,所以b+3=0,解得b=-3,所以点C(a,b)的坐标为(5,-3)。
12. 若点P(x,y)在第四象限,且|x|= 2,$y^2= 9,$则x+y的值为
-1
。
答案:
-1 【解析】因为|x|=2,y²=9,所以x=±2,y=±3。因为点P(x,y)在第四象限,所以x>0,y<0,所以x=2,y=-3,所以x+y=2+(-3)=-1。
13. 如图,已知四边形ABCD(网格中每个小正方形的边长均为1)。
(1)写出点A,B,C,D的坐标。
(2)求四边形ABCD的面积。
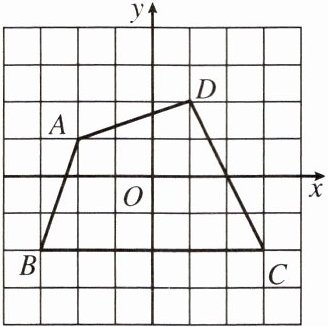
(1)写出点A,B,C,D的坐标。
(2)求四边形ABCD的面积。

答案:
解:
(1)A(-2,1),B(-3,-2),C(3,-2),D(1,2)。
(2)S四边形ABCD=3×3+2×$\frac{1}{2}$×1×3+$\frac{1}{2}$×2×4 =16。
(1)A(-2,1),B(-3,-2),C(3,-2),D(1,2)。
(2)S四边形ABCD=3×3+2×$\frac{1}{2}$×1×3+$\frac{1}{2}$×2×4 =16。
14. 已知a,b都是实数,设点P(a,b),若满足3a= 2b+5,则称点P为“新奇点”。
(1)判断点A(3,2)是否为“新奇点”,并说明理由。
(2)若点M(m-1,3m+2)是“新奇点”,请判断点M在第几象限,并说明理由。
(1)判断点A(3,2)是否为“新奇点”,并说明理由。
(2)若点M(m-1,3m+2)是“新奇点”,请判断点M在第几象限,并说明理由。
答案:
解:
(1)由A(3,2)知,3×3=9,2×2+5=4+5=9,所以3×3=2×2+5,所以A(3,2)是“新奇点”。
(2)点M在第三象限。理由如下:因为点M(m-1,3m+2)是“新奇点”,所以3(m-1)=2(3m+2)+5,解得m=-4,所以m-1=-5,3m+2=-10,所以点M在第三象限。
(1)由A(3,2)知,3×3=9,2×2+5=4+5=9,所以3×3=2×2+5,所以A(3,2)是“新奇点”。
(2)点M在第三象限。理由如下:因为点M(m-1,3m+2)是“新奇点”,所以3(m-1)=2(3m+2)+5,解得m=-4,所以m-1=-5,3m+2=-10,所以点M在第三象限。
查看更多完整答案,请扫码查看


