11. 在平面直角坐标系中,点A(2,-m+1)与点B(n+1,0)关于y轴对称,则代数式$m^2+n^2$的值为
10
。
答案:
10
12. 已知点P(2a,1-3a)在第二象限,且点P到x轴的距离与到y轴的距离之和为6,则a的值为
-1
。
答案:
-1
13. 生活中很多图案都与斐波那契数列1,1,2,3,5,8,…相关,如图,在平面直角坐标系中,依次以这组数为半径作90°的圆弧,得到一组螺旋线,若各点分别为$P_1(-1,0),P_2(0,1),P_3(1,0),…$则点$P_7$的坐标为______。
]
]
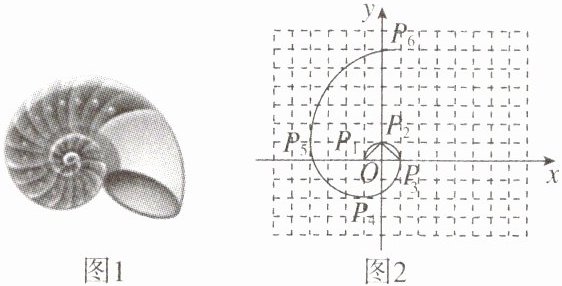
(9,-2)
答案:
(9,-2)【解析】观察发现:P₁(-1,0)先向右平移1个单位,再向上平移1个单位得到P₂(0,1);P₂(0,1)先向右平移1个单位,再向下平移1个单位得到P₃(1,0);P₃(1,0)先向左平移2个单位,再向下平移2个单位得到P₄(-1,-2);P₄(-1,-2)先向左平移3个单位,再向上平移3个单位得到P₅(-4,1);P₅(-4,1)先向右平移5个单位,再向上平移5个单位得到P₆(1,6);根据1,1,2,3,5,8,…的变化规律可知,P₆(1,6)先向右平移8个单位,再向下平移8个单位得到P₇(9,-2)。
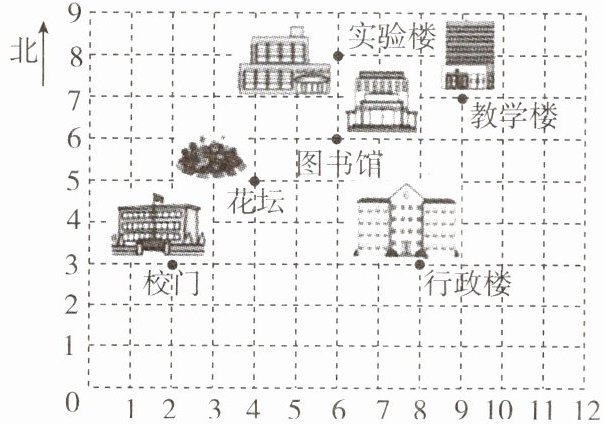
14. (10分)如图,这是某校局部分布图。如果规定列号写在前面,行号写在后面,试用数对的方法表示出图中各个地点的位置。

答案:
解:因为规定列号写在前面,行号写在后面,所以实验楼(6,8),教学楼(9,7),图书馆(6,6),花坛(4,5),行政楼(8,3),校门(2,3)。
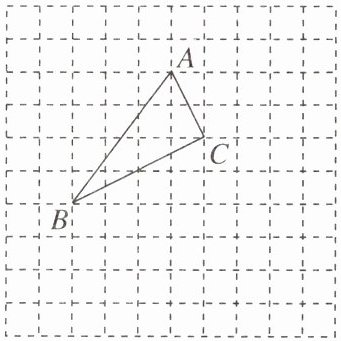
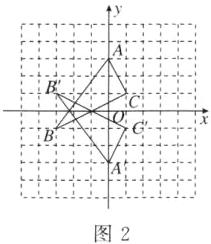
15. (11分)如图,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题。
(1)在图中建立正确的直角坐标系。
(2)根据所建立的直角坐标系,写出点B和点C的坐标。
(3)在图中画出△ABC关于x轴的对称图形△A'B'C'。
(1)在图中建立正确的直角坐标系。
(2)根据所建立的直角坐标系,写出点B和点C的坐标。
(3)在图中画出△ABC关于x轴的对称图形△A'B'C'。

答案:
(1)所建立的直角坐标系如图1所示。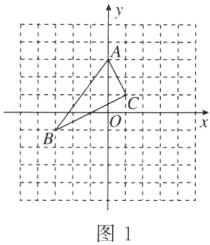
(2)点B和点C的坐标分别为B(-3,-1),C(1,1)。
(3)所求作的△A'B'C'如图2所示。
(1)所建立的直角坐标系如图1所示。


(2)点B和点C的坐标分别为B(-3,-1),C(1,1)。
(3)所求作的△A'B'C'如图2所示。
16. (14分)P(a,b)是平面直角坐标系内一点,点P的轴变换定义为:当|a|>|b|时,作点P关于x轴对称;当|a|≤|b|时,作点P关于y轴对称。根据定义,解决问题:
如图,在平面直角坐标系中,点A的坐标为(2,1),点B的坐标为(-1,m),其中m<-1,点A,B轴变换后的对应点是点A',B'。
(1)分别求A',B'的坐标。
(2)若A'B= AB',求m的值。
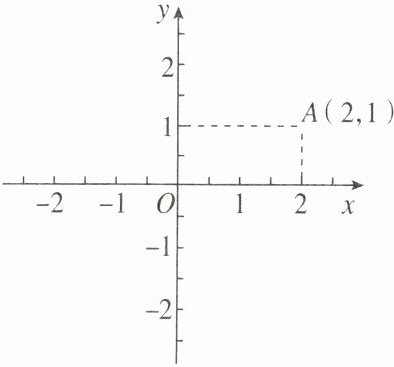
如图,在平面直角坐标系中,点A的坐标为(2,1),点B的坐标为(-1,m),其中m<-1,点A,B轴变换后的对应点是点A',B'。
(1)分别求A',B'的坐标。
(2)若A'B= AB',求m的值。

答案:
(1)由于点A(2,1),而|2|>|1|,所以点A(2,1)关于x轴对称的点为A'(2,-1);因为点B的坐标为(-1,m),其中m<-1,即|-1|<|m|,所以点B(-1,m)关于y轴对称的点为B'(1,m)。所以点A'(2,-1),点B'(1,m)。
(2)如图,点A(2,1)关于x轴的对称点A'(2,-1),点B(-1,m)关于y轴的对称点B'(1,m),延长AA',BB'相交于点C,由对称可知,AA'=BB'=2。又因为A'B=AB',A'B'=A'B',所以△AA'B≌△BB'A'(SSS),所以∠A'AB'=∠A'BB',因为A'B=AB',∠A'AB'=∠A'BB',∠C=∠C =90°,所以△AB'C≌△BA'C,所以A'C=B'C,即-1-m=2-1,解得m=-2。
(1)由于点A(2,1),而|2|>|1|,所以点A(2,1)关于x轴对称的点为A'(2,-1);因为点B的坐标为(-1,m),其中m<-1,即|-1|<|m|,所以点B(-1,m)关于y轴对称的点为B'(1,m)。所以点A'(2,-1),点B'(1,m)。
(2)如图,点A(2,1)关于x轴的对称点A'(2,-1),点B(-1,m)关于y轴的对称点B'(1,m),延长AA',BB'相交于点C,由对称可知,AA'=BB'=2。又因为A'B=AB',A'B'=A'B',所以△AA'B≌△BB'A'(SSS),所以∠A'AB'=∠A'BB',因为A'B=AB',∠A'AB'=∠A'BB',∠C=∠C =90°,所以△AB'C≌△BA'C,所以A'C=B'C,即-1-m=2-1,解得m=-2。

查看更多完整答案,请扫码查看


