1. 下列各组长度的线段能构成三角形的是(
A.1 cm,3 cm,2 cm
B.3 cm,7 cm,3 cm
C.6 cm,1 cm,6 cm
D.4 cm,10 cm,4 cm
C
)A.1 cm,3 cm,2 cm
B.3 cm,7 cm,3 cm
C.6 cm,1 cm,6 cm
D.4 cm,10 cm,4 cm
答案:
C
2. “在同一平面内,经过直线上或直线外一点,有且只有一条直线与已知直线垂直”是(
A.定义
B.定理
C.基本事实
D.已知条件
C
)A.定义
B.定理
C.基本事实
D.已知条件
答案:
C
3. 如图,图中以AB为边的三角形共有(
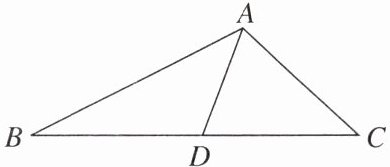
A.1个
B.2个
C.3个
D.4个
B
)
A.1个
B.2个
C.3个
D.4个
答案:
B
4. 下列图形中,线段BE是△ABC的高线的是(
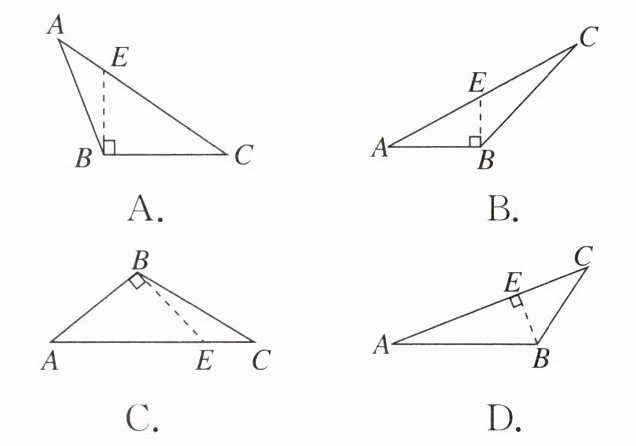
D
)
答案:
D
5. 下列选项中,可以用来说明命题“两个锐角互余”是假命题的反例是(
A.∠1= 30°,∠2= 80°
B.∠1= 0°,∠2= 50°
C.∠1= 20°,∠2= 70°
D.∠1= 20°,∠2= 120°
A
)A.∠1= 30°,∠2= 80°
B.∠1= 0°,∠2= 50°
C.∠1= 20°,∠2= 70°
D.∠1= 20°,∠2= 120°
答案:
A
6. 如图,AD,AE分别为△ABC的高线和角平分线,DF⊥AE于点F,当$∠ADF= 68°,∠C= 65°$时,∠B的度数为(
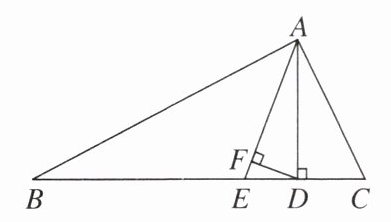
A.21°
B.23°
C.25°
D.30°
A
)
A.21°
B.23°
C.25°
D.30°
答案:
A
7. 如图,若AB//DE,BC⊥CD,α,β是两个角的度数,则下列说法正确的是(
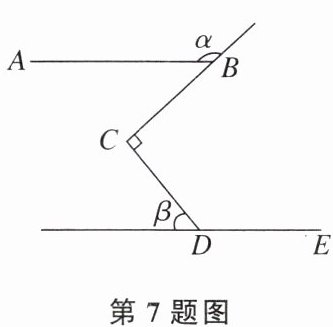
A.α,β之和为定值
B.α,β之积为定值
C.β随α的增大而减小
D.β随α的增大而增大
D
)
A.α,β之和为定值
B.α,β之积为定值
C.β随α的增大而减小
D.β随α的增大而增大
答案:
D
8. 如图,∠ABC= ∠ACB,AD,BD,CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF,有以下结论:①AD//BC,②∠ACB= ∠ADB,$③∠ADC+∠ABD= 90°,$$④∠ADB= 45°-∠CDB,$其中正确的结论有(
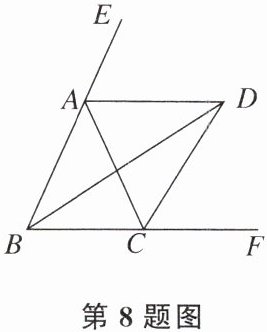
A.1个
B.2个
C.3个
D.4个
①③
)
A.1个
B.2个
C.3个
D.4个
答案:
B【解析】因为AD平分∠EAC,所以∠EAC=2∠EAD。因为∠EAC=∠ABC+∠ACB,∠ABC=∠ACB,所以∠EAD=∠ABC,所以AD//BC,故①正确;因为AD//BC,所以∠ADB=∠DBC。因为BD平分∠ABC,∠ABC=∠ACB,所以∠ABC=∠ACB=2∠DBC,所以∠ACB=2∠ADB,故②错误;在△ADC中,∠ADC+∠CAD+∠ACD=180°,因为CD平分△ABC的外角∠ACF,所以∠ACD=∠DCF。因为AD//BC,所以∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB,所以∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,所以∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,所以∠ADC+∠ABD=90°,故③正确;因为BD平分∠ABC,所以∠ABD=∠DBC。因为∠ADB=∠DBC,所以∠ABD=∠ADB。因为90°-$\frac{1}{2}$∠ABC=90°-∠ABD=∠DBC+∠BDC=∠ABD+∠BDC,所以∠BDC=90°-2∠ABD,所以∠ADB=∠ABD=45°-$\frac{1}{2}$∠CDB,④错误。
9. 命题“两个锐角的和是锐角”是
假
命题。(填“真”或“假”)
答案:
假
查看更多完整答案,请扫码查看


