《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

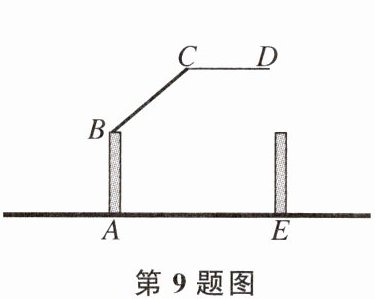
9. 车库的电动门栏杆如下图所示,BA垂直于地面AE于A,CD平行于地面AE,则$\angle ABC+\angle BCD$的大小是 ( )

A.$150^\circ$
B.$180^\circ$
C.$270^\circ$
D.$360^\circ$

答案：
C 【解析】如图,过点B作BF//AE,
因为CD//AE,
所以BF//CD,

所以 ∠BCD + ∠CBF = 180°。
因为AB⊥AE，所以AB⊥BF,
所以 ∠ABF = 90°，
所以 ∠ABC + ∠BCD = ∠ABF + ∠CBF + ∠BCD = 90° + 180° = 270°。

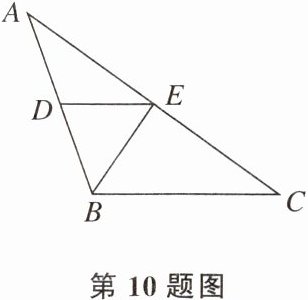
10. 如图,在$\triangle ABC$中,$\angle ABC= 110°$,$\angle C= 35°$,已知BE平分$\angle ABC$交AC于点E,过点E作$DE// BC$交AB于点D,请证明$BE\perp AC$。对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式)。
证明：因为BE平分$\angle ABC$(已知),所以$\angle EBC= \frac{1}{2}$①∠ABC(角平分线的定义)。因为$\angle ABC= 110°$(已知),所以$\angle EBC= $②55$°$(等量代换)。因为$DE// BC$(已知),所以$\angle EBC= \angle BED= $③55$°$(两直线平行,内错角相等),$\angle AED= \angle C$(④两直线平行，同位角相等)。因为$\angle C= 35°$(已知),所以$\angle AED= 35°$(等量代换)。因为$\angle AEB= $⑤∠AED$+\angle BED$,所以$\angle AEB= 35°+55°=90°$,所以$BE\perp AC$(垂直的定义)。

答案： ①∠ABC；②55；③55；④两直线平行，同位角相等；⑤∠AED

11. 下列命题是真命题还是假命题？如果你认为是假命题,请说明理由；如果你认为是真命题,请给出证明。
(1)对于所有的自然数n,$n^2$的末位数字都不是2。
(2)对于所有的自然数n,$n^2+n$的值都是偶数。

答案： 解：
(1)是真命题。证明如下：
因为 0 到 9 的平方的末位数字只能为 0，1，4，5，6，9，
所以对于所有的自然数 n，n² 的末位数字都不是 2。
(2)是真命题。证明如下：
因为 n² + n = n(n + 1)，
对于所有的自然数 n，n 与 n + 1 中必有一个为偶数，
所以对于所有的自然数 n，n² + n 的值都是偶数。

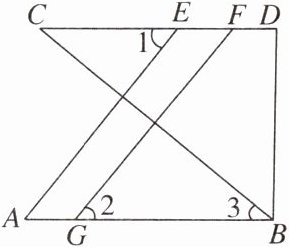
12. 如图,已知$AE\perp BC$,$FG\perp BC$,$\angle 1= \angle 2$。
(1)求证：$AB// CD$。
(2)若$\angle 3= 40^\circ$,$\angle D-\angle CBD= 40^\circ$,直接写出$\angle D$的度数。

答案： 解：
(1)证明：因为AE⊥BC，FG⊥BC，
所以AE//FG，所以∠2 = ∠A。
因为∠1 = ∠2，所以∠1 = ∠A，
所以AB//CD。
(2)因为AB//CD，所以∠C = ∠3 = 40°。
因为∠D - ∠CBD = 40°，
所以∠CBD = ∠D - 40°。
因为∠C + ∠CBD + ∠D = 180°，
所以40° + (∠D - 40°) + ∠D = 180°，
解得∠D = 90°。