《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

9. 如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且DB= DC,求证：EB= FC。

答案： 证明:因为AD平分∠BAC,DE⊥AB,DF⊥AC,所以DE=DF,∠BED=∠CFD=90°。
　在Rt△DBE和Rt△DCF中,因为{DB = DC,DE = DF},
　所以Rt△DBE≌Rt△DCF(HL),所以EB=FC。

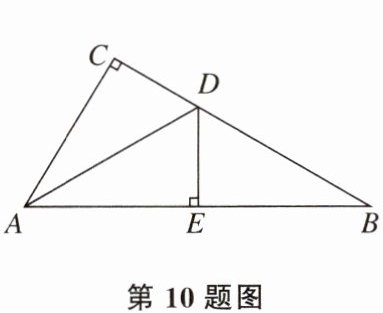
10. 如图,在△ABC中,∠C= 90°,AD是∠CAB的平分线,DE⊥AB于点E,DE平分∠ADB,则∠DBA等于 (B)

A.22.5°
B.30°
C.25°
D.40°

答案： B

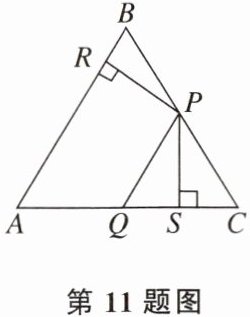
11. 如图,P,Q分别是BC,AC上的点,作PR⊥AB于点R,作PS⊥AC于点S,若AQ= PQ,PR= PS,下面三个结论：①AS= AR。②QP//AR。③△BRP≌△CSP。其中正确的结论是 (C)

A.①③
B.②③
C.①②
D.①②③

答案： C　[解析]连结AP(图略),
　　因为PR=PS,所以AP是∠BAC的平分线，
　　所以△APR≌△APS,
　　所以AS=AR,①正确。
　　因为AQ=PQ,所以∠BAP=∠QAP=∠QPA,所以QP//AR,②正确。
　　BC只是过点P,并没有固定，显然△BRP≌△CSP不一定成立。

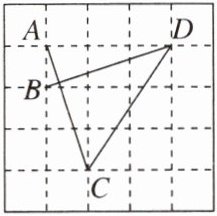
12. 如图,正方形网格中,点A,B,C,D均在格点上,则∠ACD+∠BDC= ______°。

答案：
90　[解析]在Rt△AEC和Rt△DAB中,
　　{AE = BD,EC = AD},
      所以Rt△AEC≌Rt△DAB(HL),
　　所以∠ACE=∠ABD。
　　因为∠EAC+∠ACE=90°,
　　所以∠EAC+∠ABD=90°,
　　所以∠AFB=90°,即∠CFD=90°,
　　所以∠ACD+∠BDC=90°。

13. 在△ABC中,AB= AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E。
(1)若B,C在DE的同侧(如图1),且AD= CE,求证：AB⊥AC。
(2)若B,C在DE的两侧(如图2),且AD= CE,其他条件不变,AB与AC仍垂直吗？若是,请给出证明；若不是,请说明理由。

答案： 解:
(1)证明:因为BD⊥DE,CE⊥DE,
　　所以∠ADB=∠AEC=90°。
　　在Rt△ABD和Rt△ACE中,
　　因为{AB = CA,BD = CE},
　　所以Rt△ABD≌Rt△CAE(HL),
　　所以∠DBA=∠EAC。
　　因为∠DAB+∠DBA=90°,
　　所以∠BAD+∠CAE=90°,
∠BAC=180°-(∠BAD+∠CAE)=90°,
所以AB⊥AC。
(2)AB⊥AC。理由如下:
同
(1)一样可证得Rt△ABD≌Rt△CAE,
所以∠DAB=∠ECA。
因为∠CAE+∠ECA=90°,
所以∠CAE+∠BAD=90°,即∠BAC=90°,
所以AB⊥AC。