《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

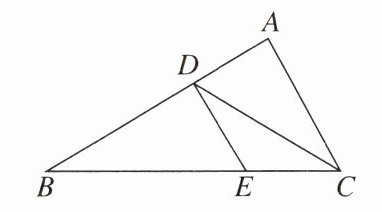
10. 如图,在△ABC中,∠A= 90°,∠B= 30°,CD平分∠ACB交AB于点D,DE//AC,交BC于点E,若AC= 3,则DE的长为(2)

A.2
$B.\frac{3}{2}$　　
$C.\frac{5}{2}$　　
D.3

答案： A 【解析】在△ABC中,∠A=90°,∠B=30°,AC=3,
所以 BC=2AC=6,∠ACB=60°。
因为 CD 平分∠ACB,所以∠ACD=∠BCD。
因为 DE//AC,
所以∠BDE=∠A=90°,∠BCD=∠ACD =∠EDC,
所以 BE=2DE,DE=CE,
所以 BC=BE+CE=3DE=6,所以 DE=2。

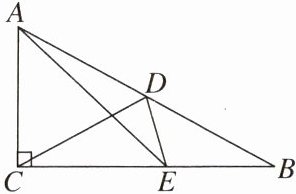
11. 如图,在Rt△ABC中,∠ACB= 90°,D为AB的中点,∠B= 30°,点E在BC上,且CE= AC,则∠CDE的大小为75°。
]

答案： 75°【解析】因为∠ACB=90°,D 是 AB 的中点,
所以 CD=AD=DB,所以∠DCB=∠B=30°,
所以 AB=2AC,
所以 CA=CD。
因为 CA=CE,
所以 CD=CE,所以∠CDE=∠CED=$\frac{1}{2}$×(180° - 30°)=75°。

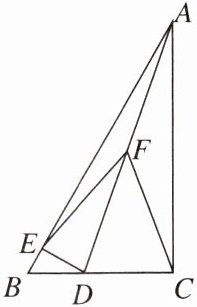
12. 如图,在△ABC中,∠ACB= 90°,D是边BC上一点,DE⊥AB于点E,F是线段AD的中点,连结EF,CF。
(1)求证：EF= CF。
(2)若∠BAC= 30°,AD= 12,求C,E两点之间的距离。
]

答案： 解:
(1)证明:因为 DE⊥AB,
所以∠DEA=90°。
在 Rt△AED 和 Rt△ACD 中,
因为 F 是斜边 AD 的中点,
所以 EF=$\frac{1}{2}$AD,CF=$\frac{1}{2}$AD,
所以 EF=CF。
(2)如图,连结 CE,
由
(1)得 EF=AF=CF=$\frac{1}{2}$AD = 6,
所以∠FEA=∠FAE,∠FCA =∠FAC,
所以∠EFC=2∠FAE+2∠FAC = 2∠BAC=2×30°=60°,
所以△EFC 是等边三角形,
所以 CE=EF=6,
所以 C,E 两点之间的距离是 6。

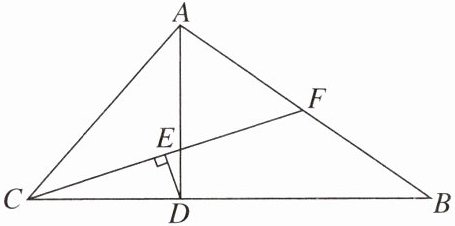
13. 如图,在△ABC中,AD是边BC上的高线,CF是边AB上的中线,且DC= BF,DE⊥CF于点E。
(1)E是CF的中点吗？请说明理由。
(2)求证：∠B= 2∠BCF。
]

答案： 解:
(1)E 是 CF 的中点。理由:如图,连结 DF。
因为 AD 是边 BC 上的高线,CF 是边 AB 上的中线,
所以 DF=BF=$\frac{1}{2}$AB。
因为 DC=BF,所以 CD =DF。
因为 DE⊥CF,所以 E 是 CF 的中点。
(2)证明:由
(1)的结论 DF=BF 得∠FDB=∠B。
因为 DC=DF,所以∠DCF=∠DFC。
由外角的性质得∠FDB=∠DCF+∠DFC = 2∠DCF,
所以∠B=2∠BCF。