10. 如图,在△ABC中,AB=AC,∠C=72°,BD平分∠ABC,BE=BC,则∠ADE的度数为 (
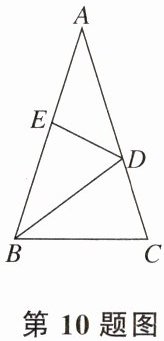
A.28°
B.36°
C.54°
D.72°
B
)
A.28°
B.36°
C.54°
D.72°
答案:
B 【解析】因为在△ABC中,AB=AC,∠C=72°, 所以∠ABC=72°,所以∠A=36°。 因为BD是∠ABC的平分线, 所以∠ABD=∠CBD= $\frac{1}{2}$∠ABC=36°。 在△BDE和△BDC中, $\left\{\begin{array}{l} BD=BD,\\ ∠ABD=∠CBD,\\ BE=BC,\end{array}\right.$ 所以△BDE≌△BDC(SAS), 所以∠BED=∠C=72°, 所以∠ADE=∠BED-∠A=36°。
11. 如图,在△ABC中,AB=AC,点D,E,F分别在BC,AC,AB上,BD=CE,CD=BF。
(1)若∠A=40°,则∠EDF=
(2)若∠A=α,则∠EDF=
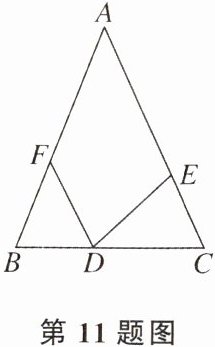
(1)若∠A=40°,则∠EDF=
70
°。 (2)若∠A=α,则∠EDF=
90°-$\frac{1}{2}$α
°。 
答案:
(1)70
(2)90°-$\frac{1}{2}$α
(1)70
(2)90°-$\frac{1}{2}$α
12. 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且AE=CD,BE与AD相交于点P,BQ⊥AD于点Q。
(1)求证:△ABE≌△CAD。
(2)求∠PBQ的度数。

(1)求证:△ABE≌△CAD。
(2)求∠PBQ的度数。

答案:
解:
(1)证明:因为△ABC为等边三角形, 所以AB=AC,∠BAC=∠ACB=60°。 在△ABE和△CAD中, 因为 $\left\{\begin{array}{l} AE=CD,\\ ∠BAC=∠ACB,\\ AB=CA,\end{array}\right.$ 所以△ABE≌△CAD(SAS)。
(2)由
(1)得,∠ABP=∠DAC, 所以∠BPQ=∠ABP+∠BAP=∠DAC+∠BAP=∠BAC=60°。 又因为BQ⊥AD,所以∠PBQ=30°。
(1)证明:因为△ABC为等边三角形, 所以AB=AC,∠BAC=∠ACB=60°。 在△ABE和△CAD中, 因为 $\left\{\begin{array}{l} AE=CD,\\ ∠BAC=∠ACB,\\ AB=CA,\end{array}\right.$ 所以△ABE≌△CAD(SAS)。
(2)由
(1)得,∠ABP=∠DAC, 所以∠BPQ=∠ABP+∠BAP=∠DAC+∠BAP=∠BAC=60°。 又因为BQ⊥AD,所以∠PBQ=30°。
13. 如图,在△ABC中,AB=AC,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连结DE。
(1)如图1,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数。
(2)如图2,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数。
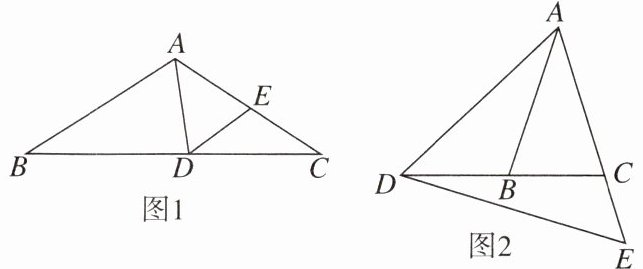
(1)如图1,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数。
(2)如图2,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数。

答案:
解:
(1)因为∠B=∠C=30°,所以∠BAC=120°。 因为∠BAD=70°,所以∠DAE=50°。 因为AD=AE,所以∠ADE=∠AED=65°, 所以∠CDE=180°-50°-30°-65°=35°。
(2)因为∠ACB=70°,∠CDE=15°, 所以∠E=70°-15°=55°。 因为AD=AE,所以∠ADE=∠AED=55°, 所以∠ADC=40°。 因为∠ABC=∠ADB+∠DAB=70°, 所以∠BAD=30°。
(1)因为∠B=∠C=30°,所以∠BAC=120°。 因为∠BAD=70°,所以∠DAE=50°。 因为AD=AE,所以∠ADE=∠AED=65°, 所以∠CDE=180°-50°-30°-65°=35°。
(2)因为∠ACB=70°,∠CDE=15°, 所以∠E=70°-15°=55°。 因为AD=AE,所以∠ADE=∠AED=55°, 所以∠ADC=40°。 因为∠ABC=∠ADB+∠DAB=70°, 所以∠BAD=30°。
查看更多完整答案,请扫码查看


