《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

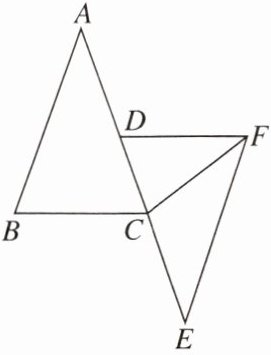
9. 如图,在△ABC中,点D,E分别在AC及其延长线上,点B,F分别在AE两侧,连结CF,已知AD= EC,BC= DF,BC//DF。求证：△ABC≌△EFD。

答案： 证明:因为AD=EC,所以AC=ED。因为BC//DF,所以$\angle ACB=\angle EDF$。在$\triangle ABC$和$\triangle EFD$中,因为$\left\{\begin{array}{l} BC=FD,\\ \angle ACB=\angle EDF,\\ AC=ED,\end{array}\right.$所以$\triangle ABC\cong \triangle EFD(SAS)$。

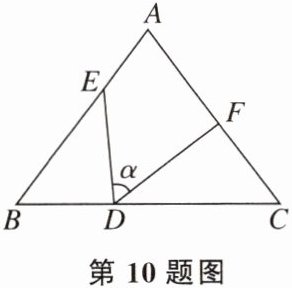
10. 如图,在△ABC中,∠B= ∠C,BD= CF,BE= CD,∠EDF= α,则下列结论正确的是(A)

A.2α+∠A= 180°
B.α+∠A= 90°
C.2α+∠A= 90°
D.α+∠A= 180°

答案： A 【解析】在$\triangle BDE$和$\triangle CFD$中,因为$\left\{\begin{array}{l} BE=CD,\\ \angle B=\angle C,\\ BD=CF,\end{array}\right.$所以$\triangle BDE\cong \triangle CFD$,所以$\angle BED=\angle CDF$。因为$\angle A+\angle B+\angle C=180^\circ$,所以$\angle B=\frac{180^\circ -\angle A}{2}$。因为$\angle BDE+\angle EDF+\angle CDF=180^\circ$,所以$180^\circ -\angle B-\angle BED+\alpha +\angle CDF=180^\circ$,所以$\angle B=\alpha$,即$\frac{180^\circ -\angle A}{2}=\alpha$,整理得$2\alpha +\angle A=180^\circ$。

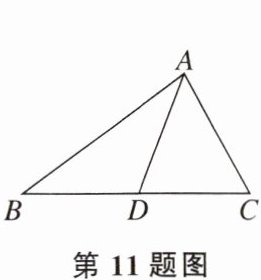
11. 在△ABC中,AB= 5,AC= 3,AD是BC边上的中线,则AD的取值范围是(C)

A.2＜AD＜8
B.3＜AD＜5
C.1＜AD＜4
D.4＜AD＜6

答案： C

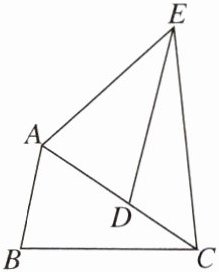
12. 如图,在△ABC中,点D是AC上一点,AD= AB,过点D作DE//AB,且DE= AC。
(1)求证：△ABC≌△DAE。
(2)若点D是AC的中点,△ABC的面积是20,求△AEC的面积。

答案：
(1)证明:因为DE//AB,所以$\angle BAC=\angle ADE$。在$\triangle ABC$和$\triangle DAE$中,$\left\{\begin{array}{l} AB=DA,\\ \angle BAC=\angle ADE,\\ DE=AC,\end{array}\right.$所以$\triangle ABC\cong \triangle DAE(SAS)$。
(2)因为$\triangle ABC\cong \triangle DAE$,所以$S_{\triangle ABC}=S_{\triangle DAE}=20$。因为点D是AC的中点,所以$S_{\triangle AEC}=2S_{\triangle DAE}=2× 20=40$。

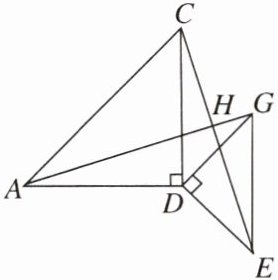
13. 如图,在△ADC和△EDG中,AD= CD,DG= DE,∠ADC= ∠GDE= 90°,连结AG,CE,相交于点H。
(1)求证：AG= CE。
(2)求∠AHE的大小。

答案：
(1)证明:因为AD=CD,DG=DE,$\angle ADC=\angle GDE=90^\circ$,所以$\angle ADC+\angle CDG=\angle GDE+\angle CDG$,即$\angle ADG=\angle CDE$,所以$\triangle ADG\cong \triangle CDE(SAS)$,所以AG=CE。
(2)设AG与CD交于点B,因为$\triangle ADG\cong \triangle CDE$,所以$\angle DAG=\angle DCE$。又因为$\angle ABD=\angle CBH$,所以$\angle CHB=\angle ADB=90^\circ$,所以$\angle AHE=90^\circ$。