1. 如图,AC与BD相交于点O,若OA= OD,用“SAS”证明△AOB≌△DOC,还需(
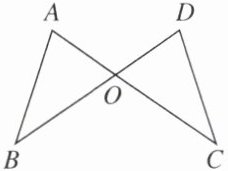
A.AB= DC
B.OB= OC
C.∠A= ∠D
D.∠AOB= ∠DOC
B
)
A.AB= DC
B.OB= OC
C.∠A= ∠D
D.∠AOB= ∠DOC
答案:
B
2. 如图,下面选项中的两个三角形全等的是(
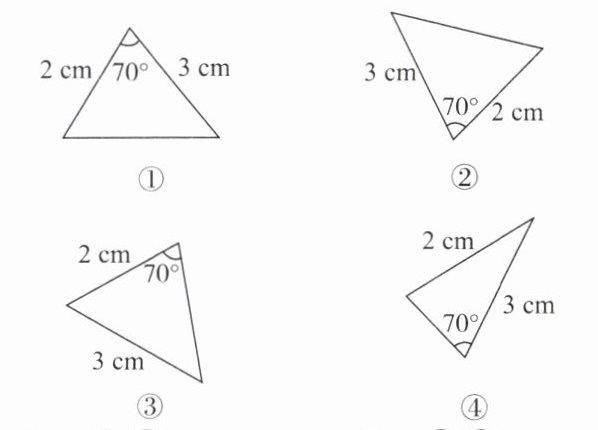
A.①②
B.②③
C.③④
D.①④
A
)
A.①②
B.②③
C.③④
D.①④
答案:
A
3. 数学课上老师布置了“测量酸奶瓶内部底面的内径”的探究任务,小熙想到了以下方案:如图,用图钉将两根吸管AD,BC的中点O固定,只要测得C,D之间的距离,就可知道内径AB的长度。此方案依据的数学定理或基本事实是(
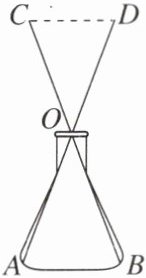
A.边边边
B.全等三角形的对应角相等
C.边角边
D.三角形的稳定性
C
)
A.边边边
B.全等三角形的对应角相等
C.边角边
D.三角形的稳定性
答案:
C
4. 如图,BD= BC,BE= CA,∠DBE= ∠C= 62°,∠BDE= 75°,则∠AFD的度数等于(
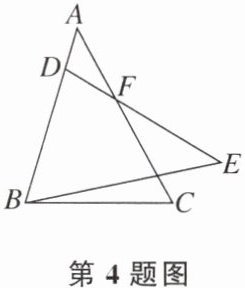
A.30°
B.32°
C.33°
D.35°
B
)
A.30°
B.32°
C.33°
D.35°
答案:
B
5. 在△ABC和△A1B1C1中,∠A= ∠A1,AB= A1B1,再补充下列哪个条件可以根据“SAS”判定△ABC和△A1B1C1全等(
A.AB= A1C1
B.BC= B1C1
C.AC= A1C1
D.AC= B1C1
C
)A.AB= A1C1
B.BC= B1C1
C.AC= A1C1
D.AC= B1C1
答案:
C
6. 如图,点A,B分别位于一个池塘的两端,C是AD的中点,也是BE的中点,若DE= 20 m,则AB=
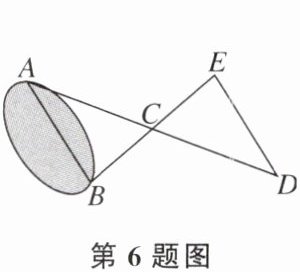
20
m。
答案:
20
7. 如图,已知方格纸中是4个相同的正方形,则∠1与∠2的和为
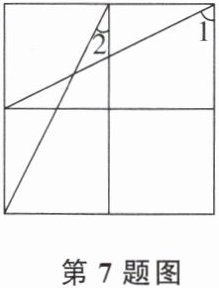
90°
。
答案:
$90^\circ$
8. 如图,已知AB⊥BD,垂足为点B,ED⊥BD,垂足为点D,若AB= CD,BC= DE,则∠ACE=
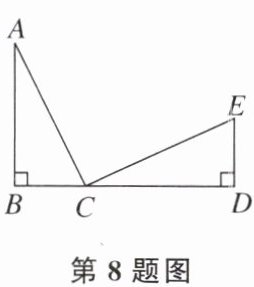
90°
。
答案:
$90^\circ$
查看更多完整答案,请扫码查看


