1. 已知△ABC为等边三角形,则∠A的度数是 (
A.30°
B.45°
C.60°
D.90°
C
)A.30°
B.45°
C.60°
D.90°
答案:
C
2. 等腰三角形的一个外角是80°,则其底角等于 (
A.40°
B.80°
C.100°
D.40°或100°
A
)A.40°
B.80°
C.100°
D.40°或100°
答案:
A
3. 如图,已知DE//BC,AB=AC,∠1=125°,则∠A的度数是 (
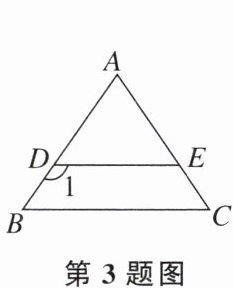
A.70°
B.45°
C.55°
D.65°
A
)
A.70°
B.45°
C.55°
D.65°
答案:
A
4. 如图,已知在Rt△ABC中,∠ACB=90°,以A为圆心,AC长为半径作弧,交AB于点D。若∠A=40°,则∠DCB的度数为 (
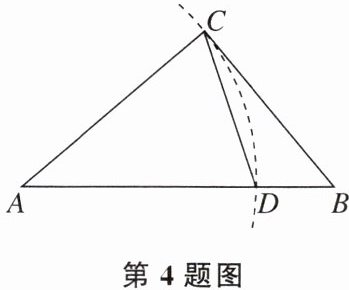
A.15°
B.20°
C.40°
D.50°
B
)
A.15°
B.20°
C.40°
D.50°
答案:
B
5. 如图,在△ABC中,AB=AC,D为AB边上一点,且AD=CD=BC,则∠A的度数为 (
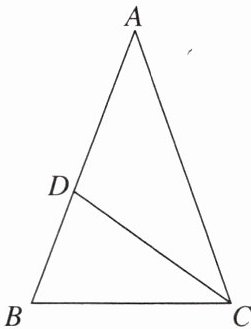
A.38°
B.36°
C.32°
D.30°
B
)
A.38°
B.36°
C.32°
D.30°
答案:
B
6. 若等腰三角形的一个角为80°,则这个等腰三角形的顶角的度数为
20°或80°
。
答案:
20°或80°
7. 若等腰三角形的顶角为86°,则腰上的高与底边所成的角的度数为
43
°。
答案:
43°
8. 如图,P,Q是△ABC的边BC上的两点,并且BP=PQ=QC=AP=AQ,求∠BAC的度数。请完善解答过程:

解:因为PQ=AP=AQ,所以△APQ是
因为BP=AP,所以∠B=∠BAP,且∠B+∠BAP=
因为QC=AQ,所以

解:因为PQ=AP=AQ,所以△APQ是
等边三角形
,所以∠PAQ=∠APQ
=∠AQP
=60°
。 因为BP=AP,所以∠B=∠BAP,且∠B+∠BAP=
60°
,所以∠B=∠BAP=30°
。 因为QC=AQ,所以
∠C=∠CAQ
,且∠C+∠CAQ
=60°,所以∠C
=∠CAQ
=30°
,所以∠BAC=∠BAP+∠PAQ+∠CAQ
=120°
。
答案:
等边三角形 ∠APQ ∠AQP 60° 60° 30° ∠C=∠CAQ ∠C+∠CAQ ∠C ∠CAQ 30° ∠BAP+∠PAQ+∠CAQ 120°
9. 如图,在△ABC中,AB=AC,∠A=30°,BD是△ABC的角平分线,求∠ADB的度数。
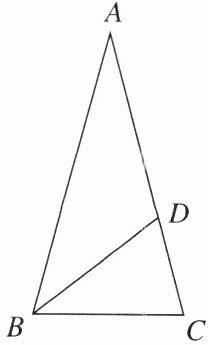

答案:
解:因为AB=AC,∠A=30°, 所以∠ABC=∠C=(180°-30°)÷2=75°。 又因为BD为∠ABC的平分线, 所以∠ABD=37.5°, 所以∠ADB=180°-(30°+37.5°)=112.5°。
查看更多完整答案,请扫码查看


