搜索
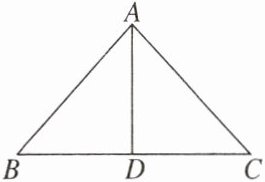
12. 如图,在△ABC中,AB= AC,AD为△BAC的角平分线,且AD= 4,若△ABD的周长为12,则△ABC的周长是
16
。
答案：
12.16
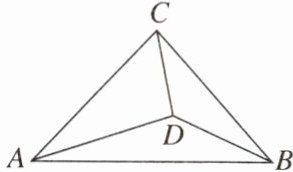
13. 如图,在等腰直角三角形ABC中,AC= BC,D为△ABC内一点,且∠BCD= ∠CAD,若CD= 4,则△BCD的面积为______。
答案：
13.8 [解析]如图,过点B作BH⊥CD,交CD的延长线于H。
因为在等腰直角三角形ABC中,AC=BC,所以∠ACB=90°。因为∠BCD=∠CAD,所以∠ACB=∠BCD+∠ACD=∠CAD+∠ACD=90°,所以∠ADC=90°,所以∠ACB=∠ADC=∠H=90°。在△ACD和△CBH中,因为{∠CAD=∠BCD,∠ADC=∠H,AC=CB,所以△ACD≌△CBH(AAS),所以BH=CD=4,所以S△BCD=$\frac{1}{2}$CD·BH=$\frac{1}{2}$×4×4=8。
13.8 [解析]如图,过点B作BH⊥CD,交CD的延长线于H。
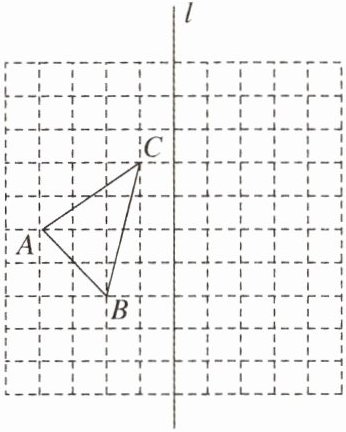
因为在等腰直角三角形ABC中,AC=BC,所以∠ACB=90°。因为∠BCD=∠CAD,所以∠ACB=∠BCD+∠ACD=∠CAD+∠ACD=90°,所以∠ADC=90°,所以∠ACB=∠ADC=∠H=90°。在△ACD和△CBH中,因为{∠CAD=∠BCD,∠ADC=∠H,AC=CB,所以△ACD≌△CBH(AAS),所以BH=CD=4,所以S△BCD=$\frac{1}{2}$CD·BH=$\frac{1}{2}$×4×4=8。 14. (10分)如图,在边长为1个单位长度的小正方形组成的网格中,点A,B,C在小正方形的顶点上。
(1)在图中画出与△ABC关于直线l成轴对称的△A'B'C'。
(2)在直线l上找一点Q,使得BQ= AQ。
(1)在图中画出与△ABC关于直线l成轴对称的△A'B'C'。
(2)在直线l上找一点Q,使得BQ= AQ。
答案：
14.解:
(1)如图1,△A'B'C'即为所求。
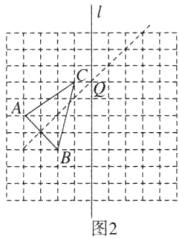
(2)如图2,作线段AB的垂直平分线交l于点Q,则点Q即为所求的点。
14.解:
(1)如图1,△A'B'C'即为所求。
(2)如图2,作线段AB的垂直平分线交l于点Q,则点Q即为所求的点。
15. (10分)如图,在△ABC中,AB= AC,点D在BC边上,且AB= BD,AD= CD,求∠B的度数。
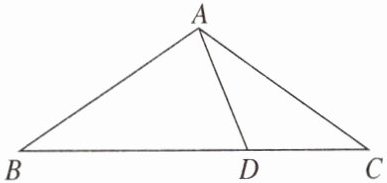
答案：
15.解:因为AB=AC,所以∠B=∠C。因为CD=DA,所以∠C=∠DAC。因为BA=BD,所以∠BDA=∠BAD=2∠C=2∠B。又因为∠B+∠BAD+∠BDA=180°,所以5∠B=180°,所以∠B=36°。
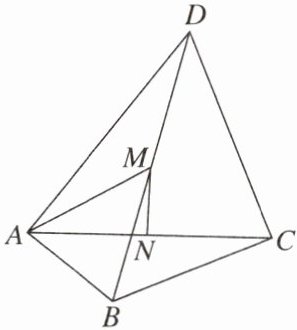
16. (15分)如图,在四边形ABCD中,∠BAD= ∠BCD= 90°,BC= 6,CD= AC= 8,M,N分别是对角线BD,AC的中点,连结AM。
(1)求AM的长。
(2)求证:MN⊥AC。
(3)求MN的长。
(1)求AM的长。
(2)求证:MN⊥AC。
(3)求MN的长。
答案：
16.解:
(1)如图，连结CM,因为∠BAD=∠BCD=90°,M是BD的中点,所以AM=CM=BM=DM=$\frac{1}{2}$BD。
因为BC=6,CD=8,所以BD=√(BC²+CD²)=10,所以AM=5。
(2)证明:因为∠BAD=∠BCD=90°,M是BD的中点,所以AM=CM=$\frac{1}{2}$BD。因为N是AC的中点,所以MN⊥AC。
(3)因为AC=8,N是AC的中点,所以AN=$\frac{1}{2}$×8=4,所以MN=√(AM² - AN²)=√(5² - 4²)=3。
16.解:
(1)如图，连结CM,因为∠BAD=∠BCD=90°,M是BD的中点,所以AM=CM=BM=DM=$\frac{1}{2}$BD。
因为BC=6,CD=8,所以BD=√(BC²+CD²)=10,所以AM=5。(2)证明:因为∠BAD=∠BCD=90°,M是BD的中点,所以AM=CM=$\frac{1}{2}$BD。因为N是AC的中点,所以MN⊥AC。
(3)因为AC=8,N是AC的中点,所以AN=$\frac{1}{2}$×8=4,所以MN=√(AM² - AN²)=√(5² - 4²)=3。
查看更多完整答案，请扫码查看
