9. 如图,以直线l为对称轴,画出轴对称图形的另一半。
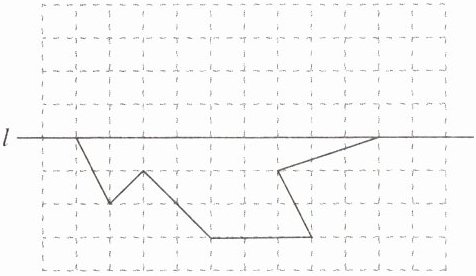

答案:
解:画图如下。
解:画图如下。

10. 如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,图中的△ABC为格点三角形,在图中与△ABC成轴对称的格点三角形可以画出 ( )
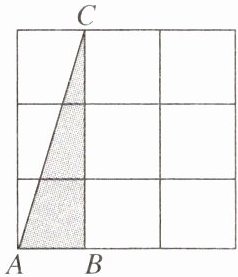
A.6个
B.5个
C.4个
D.3个

A.6个
B.5个
C.4个
D.3个
答案:
A 【解析】如图,最多能画出 6 个与△ABC 成轴对称的格点三角形。
A 【解析】如图,最多能画出 6 个与△ABC 成轴对称的格点三角形。

11. 如图,在△ABC中,∠ACB= 90°,AC= 12,BC= 9,P是AB上的一个动点(不与点B重合)。点B与点B′关于直线PC对称,连结CB′,AB′,PB′,则线段AB′长度的最小值是
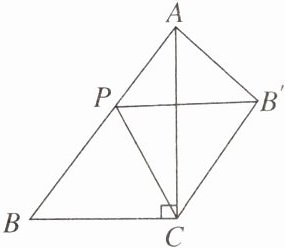
3
。
答案:
3 【解析】根据题意,得 CB'=CB=9。因为 CB'+AB'≥AC,所以当 A,B',C 三点共线时,线段 AB'的长度取得最小值。因为 AC=12,所以 AB'=AC - BC=3。
12. 如图,△ABC和△ABE关于直线AB对称,△ABC和△ADC关于直线AC对称,CD与AE交于F,若∠ABC= 32°,∠ACB= 18°,则∠CFE=
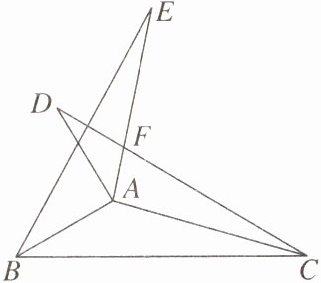
118°
。
答案:
118° 【解析】因为△ABC 和△ABE 关于直线 AB 对称,△ABC 和△ADC 关于直线 AC 对称,所以∠DCA=∠ACB=18°,∠BAC=∠BAE。因为∠ABC=32°,所以∠BAC=180° - 18° - 32°=130°,所以∠EAC=360° - 130° - 130°=100°,所以∠CFE=∠ACD+∠EAC=18°+100°=118°。
13. 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点三角形ABC(即三角形的顶点都在格点上)。
(1)求△ABC的面积。
(2)在图中作出与△ABC关于直线MN成轴对称的△A′B′C′。
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短。(保留作图痕迹)
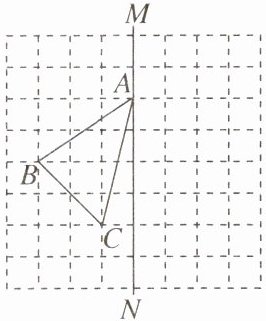
(1)求△ABC的面积。
(2)在图中作出与△ABC关于直线MN成轴对称的△A′B′C′。
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短。(保留作图痕迹)

答案:
解:
(1)S△ABC=3×4 - $\frac{1}{2}$×2×2 - $\frac{1}{2}$×1×4 - $\frac{1}{2}$×2×3=12 - 2 - 2 - 3=5。
(2)如图,△A'B'C'即为所求。
(3)如图,连结 BC',交直线 MN 于点 P,点 P 即为所求。
解:
(1)S△ABC=3×4 - $\frac{1}{2}$×2×2 - $\frac{1}{2}$×1×4 - $\frac{1}{2}$×2×3=12 - 2 - 2 - 3=5。
(2)如图,△A'B'C'即为所求。
(3)如图,连结 BC',交直线 MN 于点 P,点 P 即为所求。

查看更多完整答案,请扫码查看


