搜索
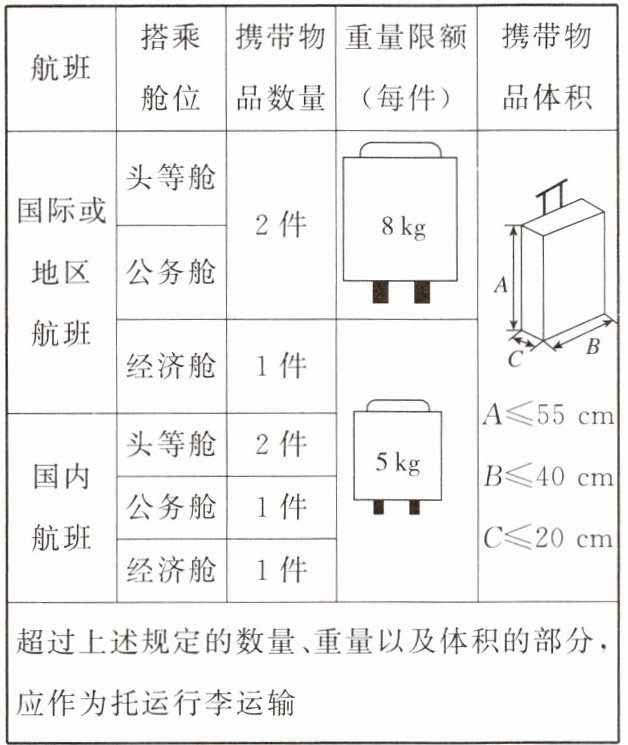
10. 数学的应用无处不在,如图,某机场的告示牌中,提示随身携带行李的规则,其中提到每件行李的重量限额为“$\leq8$千克”,则将表示行李限额(每件)的不等式表示在数轴上为(
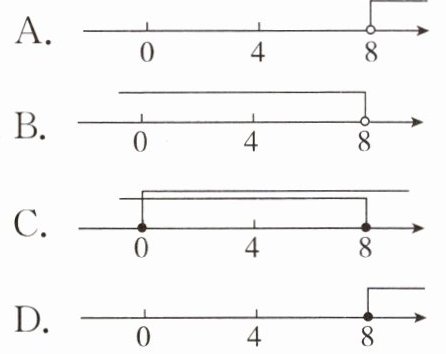
C
)
答案：
C
11. 根据机器零件的设计图纸(如图),用不等式表示零件长度的合格尺寸($L$的取值范围)：
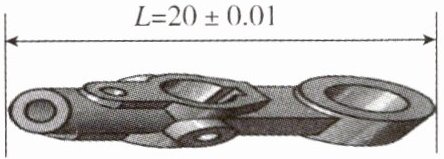
$19.99 \leqslant L \leqslant 20.01$
。
答案：
$19.99 \leqslant L \leqslant 20.01$
12. (1)在数轴上表示不等式$-3\leq x＜6$,并写出在$-3\leq x＜6$范围内的所有整数。
（2）观察数轴确定下列实数：$-4$，$-2$，$0$，$4\frac{1}{2}$，$7$，其中只有_____不在$-3\leqslant x\lt6$范围内。
（2）观察数轴确定下列实数：$-4$，$-2$，$0$，$4\frac{1}{2}$，$7$，其中只有_____不在$-3\leqslant x\lt6$范围内。
答案：
解:
(1)
-3,-2,-1,0,1,2,3,4,5。
(2)−4,7
解:
(1)
-3,-2,-1,0,1,2,3,4,5。(2)−4,7
13. 在数轴上有$A$,$B$两点,其中点$A所对应的数是a$,点$B$所对应的数是1。已知$A$,$B$两点间的距离小于3,请你利用数轴解答。
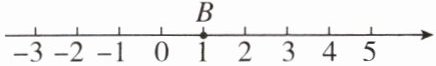
(1)直接写出$a$的取值范围。
(2)数$-3$,$0$,$4所对应的点到点B$的距离小于3吗？
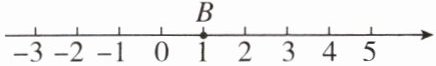
(1)直接写出$a$的取值范围。
(2)数$-3$,$0$,$4所对应的点到点B$的距离小于3吗？
答案：
解:
(1)因为1 - 3 = -2,1 + 3 = 4,所以a的取值范围是$-2 ＜ a ＜ 4$。
(2)因为$|-3 - 1| = 4,4 ＞ 3$,$|0 - 1| = 1,1 ＜ 3$,$|4 - 1| = 3,3 = 3$,所以只有数0所对应的点到点B的距离小于3。
(1)因为1 - 3 = -2,1 + 3 = 4,所以a的取值范围是$-2 ＜ a ＜ 4$。
(2)因为$|-3 - 1| = 4,4 ＞ 3$,$|0 - 1| = 1,1 ＜ 3$,$|4 - 1| = 3,3 = 3$,所以只有数0所对应的点到点B的距离小于3。
查看更多完整答案，请扫码查看
