1. 在证明过程中,不能用来作为推理依据的是 (
A.基本事实
B.定理
C.定义
D.命题
D
)A.基本事实
B.定理
C.定义
D.命题
答案:
D
2. 公元前3世纪,古希腊数学家欧几里得编写了《几何原本》。他在编写这本书时挑选一部分数学名词和公认的真命题(即公理)作为证实其他命题的出发点和依据,除公理外,其他命题的真假都需要通过演绎推理的方法进行判断。在此基础上,逐渐形成了一种重要的数学思想。这种思想是 (
A.公理化思想
B.数形结合思想
C.分类讨论思想
D.转化思想
A
)A.公理化思想
B.数形结合思想
C.分类讨论思想
D.转化思想
答案:
A
3. 如图,直线a,b被直线c所截,下列条件中不能判定直线a与b平行的是 (
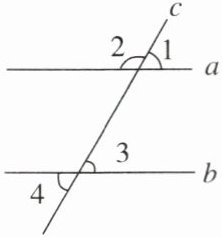
A.$\angle 1= \angle 3$
B.$\angle 2+\angle 4= 180^\circ$
C.$\angle 1= \angle 4$
D.$\angle 3= \angle 4$
D
)
A.$\angle 1= \angle 3$
B.$\angle 2+\angle 4= 180^\circ$
C.$\angle 1= \angle 4$
D.$\angle 3= \angle 4$
答案:
D
4. 如图,在数学课上,老师画一条直线a,按图中所示的方法,画一条直线b与直线a平行,再向上推三角尺,画一条直线c也与直线a平行,此时,发现直线b与直线c也平行,这就说明了 (
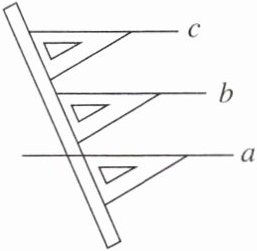
A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行
B.两直线平行,同位角相等
C.同旁内角相等,两直线平行
D.过直线外一点,有且只有一条直线与已知直线平行
A
)
A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行
B.两直线平行,同位角相等
C.同旁内角相等,两直线平行
D.过直线外一点,有且只有一条直线与已知直线平行
答案:
A
5. 如图,$AB// CD$,CE平分$\angle BCD$,$\angle B= 40°$,则$\angle DCE$等于 (
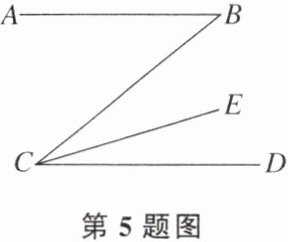
A.$20^\circ$
B.$36^\circ$
C.$45^\circ$
D.$54^\circ$
A
)
A.$20^\circ$
B.$36^\circ$
C.$45^\circ$
D.$54^\circ$
答案:
A
6. 下列各项:①基本事实。②已学定理。③定义。④等量代换。⑤不等式性质。⑥度量结果。⑦已知条件。⑧正确的观察结果。⑨猜测结果。其中,可以作为推理依据的是
①②③④⑤⑦
。(填序号)
答案:
①②③④⑤⑦
7. “因为$\angle A+\angle B= 90°$,$\angle A+\angle C= 90°$,所以$\angle B= \angle C$。”这一推理的依据是
同角的余角相等
。
答案:
同角的余角相等
8. 如图,$\angle E= 52°$,$\angle BAC= 52°$,$\angle D= 110°$,求$\angle ABD$的度数。请完善解答过程,并在括号内填写相应的理论依据。
解:因为$\angle E= 52°$,$\angle BAC= 52°$(已知),所以$\angle E=$
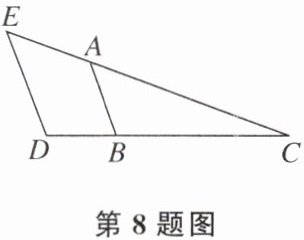
解:因为$\angle E= 52°$,$\angle BAC= 52°$(已知),所以$\angle E=$
∠BAC
(等量代换),所以AB
$//$ED
(同位角相等,两直线平行
),所以∠ABD
$+\angle D= 180°$(两直线平行,同旁内角互补
)。因为$\angle D= 110°$(已知),所以$\angle ABD= 70°$(等式的性质)。 
答案:
∠BAC AB ED 同位角相等,两直线平行 ∠ABD 两直线平行,同旁内角互补
查看更多完整答案,请扫码查看


