【例 2】【问题情境】如图,在△ABC中,AB= BC,∠ABC>90°,CD与直线AB垂直,垂足为D,∠BCD的平分线CE交BD于点E,点H在线段AC上,HE的延长线与CD的延长线相交于点F。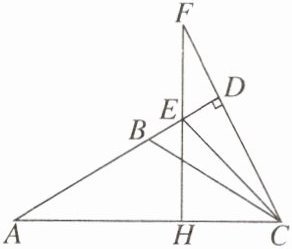
【探索求证】(1)求证:∠ACE= 45°。
【深入探究】(2)若FH⊥AC,请判断CF与AE有怎样的数量关系,并说明理由。

【探索求证】(1)求证:∠ACE= 45°。
【深入探究】(2)若FH⊥AC,请判断CF与AE有怎样的数量关系,并说明理由。
答案:
(1)证明:因为AB=BC,所以∠A=∠ACB。因为CE平分∠BCD,所以∠BCE=∠DCE。因为CD⊥直线AB,所以∠ADC=90°,所以∠A+∠ACB+∠BCE+∠DCE=90°,即2(∠ACB+∠BCE)=90°,所以∠ACB+∠BCE=45°,即∠ACE=45°。
(2)CF=AE,理由:因为FH⊥AC,所以∠EHC=90°。又因为∠ACE=45°,所以∠HEC=45°,所以△EHC为等腰直角三角形,所以EH=CH。因为FH⊥AC,所以∠EHA=∠EHC=90°,所以∠F+∠ACD=90°。因为∠ADC=90°,所以∠A+∠ACD=90°,所以∠A=∠F,所以△AEH≌△FCH(AAS),所以CF=AE。
(1)证明:因为AB=BC,所以∠A=∠ACB。因为CE平分∠BCD,所以∠BCE=∠DCE。因为CD⊥直线AB,所以∠ADC=90°,所以∠A+∠ACB+∠BCE+∠DCE=90°,即2(∠ACB+∠BCE)=90°,所以∠ACB+∠BCE=45°,即∠ACE=45°。
(2)CF=AE,理由:因为FH⊥AC,所以∠EHC=90°。又因为∠ACE=45°,所以∠HEC=45°,所以△EHC为等腰直角三角形,所以EH=CH。因为FH⊥AC,所以∠EHA=∠EHC=90°,所以∠F+∠ACD=90°。因为∠ADC=90°,所以∠A+∠ACD=90°,所以∠A=∠F,所以△AEH≌△FCH(AAS),所以CF=AE。
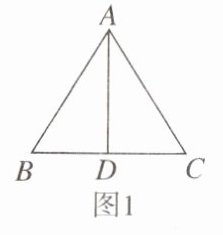
【变式】【数学知识】等腰三角形的“三线合一”性质非常重要。如图 1,在△ABC中,AB= AC,AD是中线,若∠C= 58°,则∠BAD的度数为
32°
。
答案:
32°
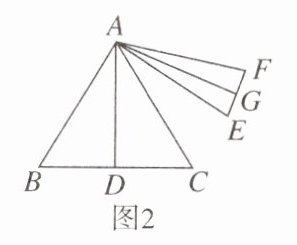
【数学应用】如图 2,在△ABC和△AEF中,AB= AC,AE= AF,AD,AG分别为△ABC和△AEF的中线,若∠BAF= 110°,∠CAE= 24°,求∠DAG的度数。

答案:
67°
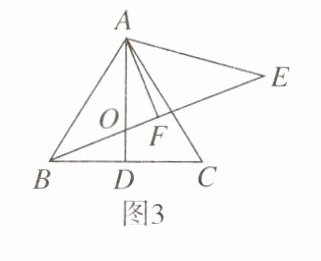
【拓展】如图 3,在△ABC和△ABE中,AB= AC,AB= AE,AD,AF分别为△ABC和△ABE的中线,AD与BE交于点O,若∠AOF= 69°,则∠CAE的度数为
42°
。
答案:
42°
查看更多完整答案,请扫码查看


