《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

【例 1】根据引入概念,理解应用概念。

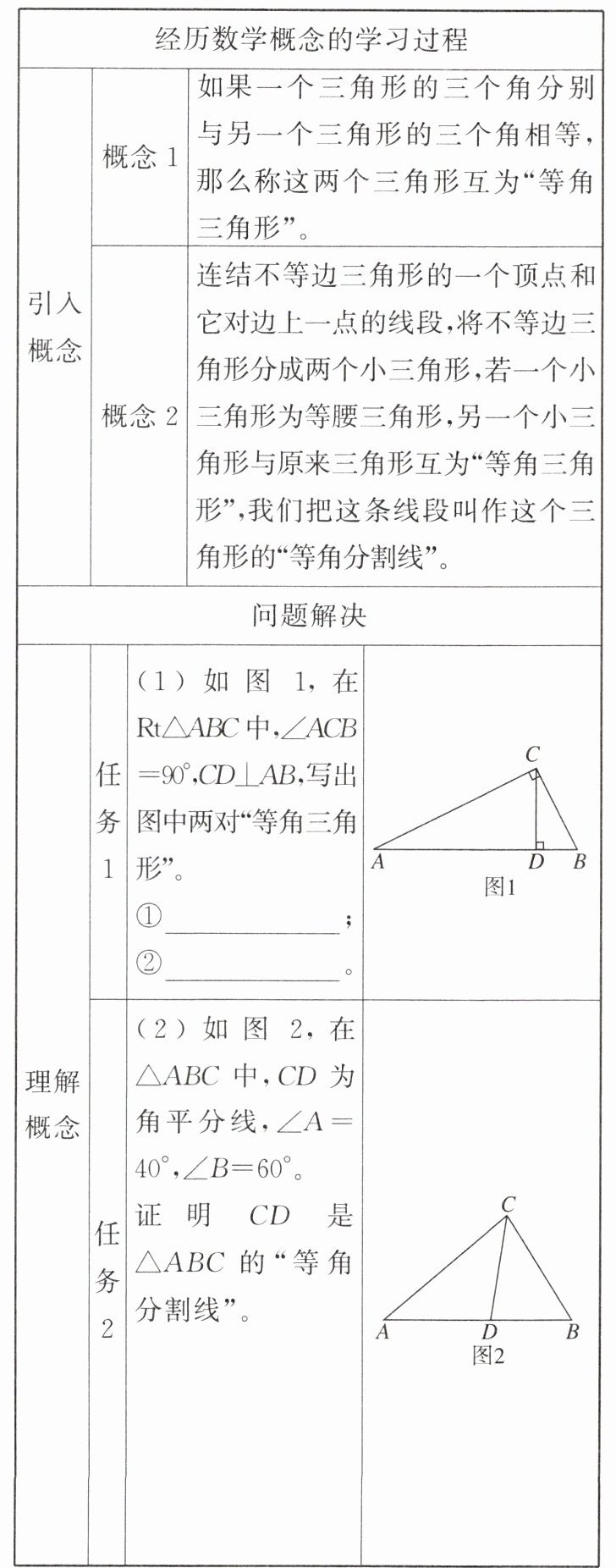
任务1:
(1)①△ACD与△CBD;②△ABC与△ACD(答案不唯一)。任务2:
(2)证明:因为∠A=40°,∠B=60°,所以∠ACB=180°-∠A-∠B=80°。因为CD为角平分线,所以∠ACD=∠BCD=40°,所以∠ACD=∠A,所以CD=AD,所以△ACD是等腰三角形。因为∠ADC=180°-∠A-∠ACD=180°-40°-40°=100°,所以∠BDC=180°-100°=80°,所以∠BDC=∠ACB,∠B=∠B,所以△ABC与△CBD是"等角三角形",所以CD为△ABC的"等角分割线"。

答案： 任务1:
(1)①△ACD与△CBD;②△ABC与△ACD(答案不唯一)。任务2:
(2)证明:因为∠A=40°,∠B=60°,所以∠ACB=180°-∠A-∠B=80°。因为CD为角平分线,所以∠ACD=∠BCD=40°,所以∠ACD=∠A,所以CD=AD,所以△ACD是等腰三角形。因为∠ADC=180°-∠A-∠ACD=180°-40°-40°=100°,所以∠BDC=180°-100°=80°,所以∠BDC=∠ACB,∠B=∠B,所以△ABC与△CBD是"等角三角形",所以CD为△ABC的"等角分割线"。

【变式】某学习小组参照教材上的材料进行勾股定理的项目式探究,并制表如下：

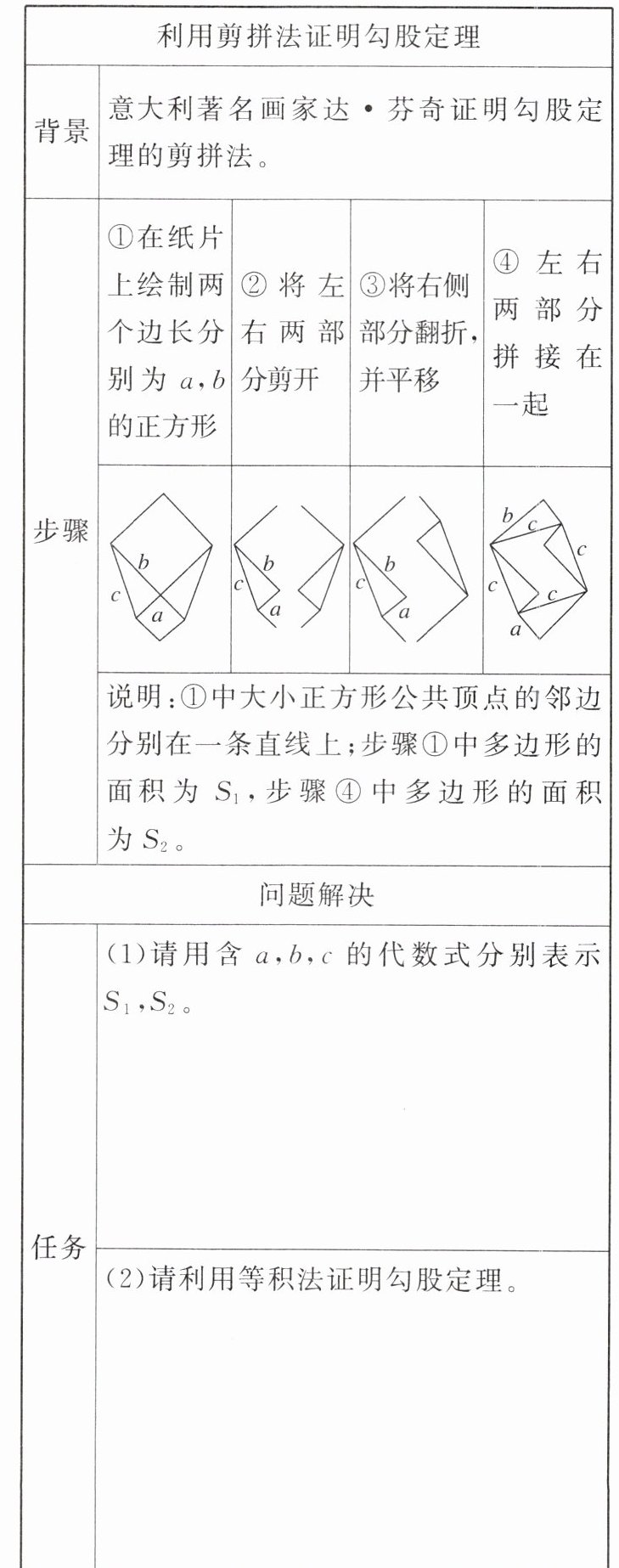
答案：
(1)S₁=a²+b²+ab，S₂=c²+ab。
(2)由S₁=S₂得a²+b²+ab=c²+ab，所以a²+b²=c²。