《2025年精彩练习就练这一本八年级数学上册浙教版评议教辅》

【例 1】足球是世界第一运动,能激发人们的热情,释放和寄托人们的情感。足球不仅是一项运动,更是一种文化,深刻地影响着人们的生活和社会的发展。下表是某商家连续两天销售 A,B 两种足球的情况：

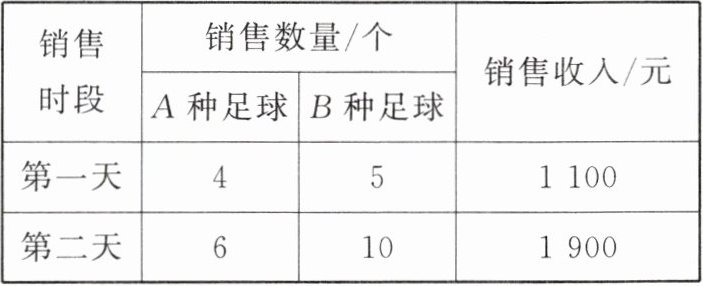
(1)求 A,B 两种足球每个的售价分别是多少。
(2)若 A,B 两种足球每个进价分别为120 元、80 元,商家决定再采购 A,B 足球共 30 个,购买金额不超过 3400 元,求 A种足球最多能采购多少个。
(3)在(2)的条件下,商店销售完这30 个足球的利润不低于 835 元,那么有哪几种采购方案？

答案： 【例1】解:
(1)设A,B两种足球每个的售价分别是x元,y元,
根据题意得,$\left\{\begin{array}{l} 4x+5y=1100,\\ 6x+10y=1900,\end{array}\right. $
解得$\left\{\begin{array}{l} x=150,\\ y=100。\end{array}\right. $
答:A,B两种足球每个的售价分别是150元、100元。
(2)设A种足球采购x个,则B种足球采购(30-x)个,
根据题意得,$120x+80(30-x)\leqslant 3400,$
解得$x\leqslant 25$。
答:A种足球最多能采购25个。
(3)根据题意得,$(150-120)x+(100-80)(30-x)\geqslant 835,$
解得$x\geqslant 23.5,$
又因为$x\leqslant 25$,且x是整数,
所以当$x=24$时,$30-x=6$;当$x=25$时,$30-x=5$。
答:共有2种采购方案:①采购A足球24个、B足球6个;②采购A足球25个、B足球5个。

【变式】照明灯具经过多年的发展,大致历经白炽灯、节能灯、LED 灯三个阶段,目前性价比最高的是 LED 灯,不仅节能,而且寿命更长,同时也更加环保。某商场计划购进甲、乙两种型号 LED 照明灯共 200 只,这两种照明灯的进价、售价如下表所示：

(1)若购进甲、乙两种型号照明灯共用去7200 元,求甲、乙两种型号照明灯各购进多少只。
(2)若商场准备用不多于8400 元购进这两种型号照明灯,问甲型号的照明灯至少购进多少只？
(3)在(2)的条件下,该商场销售完200 只照明灯后能否实现盈利不低于2390 元的目标？若能,请你给出相应的采购方案；若不能,请说明理由。

答案： 【变式】解:
(1)设购进甲型号LED照明灯x只,乙型号LED照明灯y只,
根据题意得$\left\{\begin{array}{l} x+y=200,\\ 30x+60y=7200,\end{array}\right. $解得$\left\{\begin{array}{l} x=160,\\ y=40。\end{array}\right. $
答:购进甲型号LED照明灯160只,乙型号LED照明灯40只。
(2)设购进甲型号LED照明灯m只,则购进乙型号LED照明灯(200-m)只,
根据题意得$30m+60(200-m)\leqslant 8400,$
解得$m\geqslant 120,$
所以m的最小值为120。
答:甲型号LED照明灯至少购进120只。
(3)根据题意得$(40-30)m+(75-60)(200-m)\geqslant 2390,$
解得$m\leqslant 122,$
又因为$m\geqslant 120$,且m为正整数,
所以m可以为120,121,122。
答:该商场销售完200只照明灯后能实现盈利不低于2390元的目标,共有3种采购方案。
方案1:购进甲型号LED照明灯120只,乙型号LED照明灯80只;
方案2:购进甲型号LED照明灯121只,乙型号LED照明灯79只。
方案3:购进甲型号LED照明灯122只,乙型号LED照明灯78只。