第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
6. 如图23.1-22,已知正方形ABCD,把边DC绕点D顺时针旋转30°到DC'处,连接AC',BC',CC'.写出图中所有的等腰三角形,并写出推理过程.
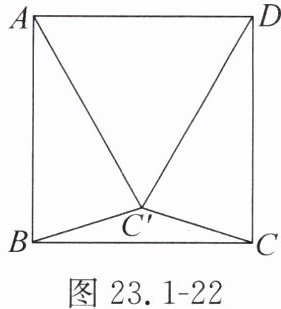

答案:
解:题图中所有的等腰三角形为△DCC',△DC'A,△C'AB,△C'BC.理由如下:
∵ 四边形ABCD为正方形,
∴ AB=AD=DC,∠BAD=∠ADC=90°,
∴ DC=DC'=DA,
∴ △DCC',△DC'A为等腰三角形.
∵ ∠C'DC=30°,∠ADC=90°,
∴ ∠ADC'=60°,
∴ △AC'D为等边三角形,
∴ AC'=AD=AB,
∴ △C'AB为等腰三角形.
∵ ∠C'AB=90°−60°=30°,
∴ ∠CDC'=∠C'AB.
在△DCC'和△ABC'中,
$\left\{\begin{array}{l} CD=BA,\\ ∠CDC'=∠BAC',\\ C'D=C'A,\end{array}\right.$
∴ △DCC'≌△ABC'(SAS),
∴ CC'=C'B,
∴ △BCC'为等腰三角形.
∵ 四边形ABCD为正方形,
∴ AB=AD=DC,∠BAD=∠ADC=90°,
∴ DC=DC'=DA,
∴ △DCC',△DC'A为等腰三角形.
∵ ∠C'DC=30°,∠ADC=90°,
∴ ∠ADC'=60°,
∴ △AC'D为等边三角形,
∴ AC'=AD=AB,
∴ △C'AB为等腰三角形.
∵ ∠C'AB=90°−60°=30°,
∴ ∠CDC'=∠C'AB.
在△DCC'和△ABC'中,
$\left\{\begin{array}{l} CD=BA,\\ ∠CDC'=∠BAC',\\ C'D=C'A,\end{array}\right.$
∴ △DCC'≌△ABC'(SAS),
∴ CC'=C'B,
∴ △BCC'为等腰三角形.
7. 如图23.1-23所示,△ABC为等边三角形,矩形ACDE与矩形ABGF的宽AE与AF相等,试问:矩形ABGF能否经过旋转到达矩形ACDE的位置?如果能,请指出旋转中心和旋转角度;如果不能,请说明理由.
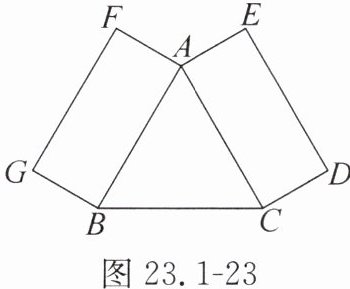

答案:
解:能(如图).
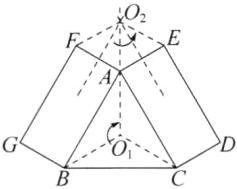
(1)以等边△ABC的中心O₁为旋转中心,将矩形ABGF绕点O₁顺时针旋转120°与矩形CAED重合;
(2)以AF,AE的垂直平分线的交点O₂为旋转中心,将矩形ABGF 绕O₂逆时针旋转60°与矩形EDCA重合.
解:能(如图).

(1)以等边△ABC的中心O₁为旋转中心,将矩形ABGF绕点O₁顺时针旋转120°与矩形CAED重合;
(2)以AF,AE的垂直平分线的交点O₂为旋转中心,将矩形ABGF 绕O₂逆时针旋转60°与矩形EDCA重合.
如图23.1-24,在Rt△ABC中,四边形DECF是正方形.
(1)请简述图①经过怎样的变换形成图②;
(2)当AD= 5,BD= 6时,设△ADE,△BDF的面积分别为$S_1,S_2,$求$S_1+S_2$的值.
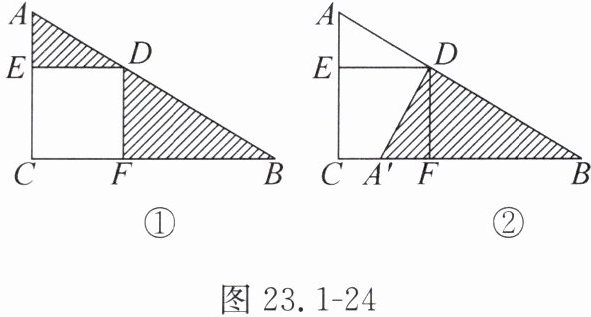
(1)请简述图①经过怎样的变换形成图②;
(2)当AD= 5,BD= 6时,设△ADE,△BDF的面积分别为$S_1,S_2,$求$S_1+S_2$的值.

答案:
解:
(1)将△ADE绕点D逆时针旋转90°形成图②;
(2)S₁+S₂=S_{△A'BD}=$\frac{1}{2}×$DA'·BD=$\frac{1}{2}$AD·BD=$\frac{1}{2}×5×6=15$.
(1)将△ADE绕点D逆时针旋转90°形成图②;
(2)S₁+S₂=S_{△A'BD}=$\frac{1}{2}×$DA'·BD=$\frac{1}{2}$AD·BD=$\frac{1}{2}×5×6=15$.
查看更多完整答案,请扫码查看


