《2025年能力培养与测试九年级数学上册人教版》

【延伸·探索】已知二次函数 $ y = x^{2} - 3 $ 的图象如图22.1 - 8所示。

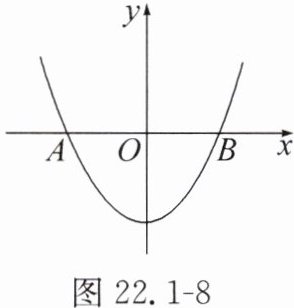
(1)画出二次函数 $ y = x^{2} - 3 $ 关于 $ x $ 轴对称的图象；
(2)求新图象对应的函数解析式。
【解答】

答案：
（1）所求的函数图象为如图所示的虚线, （2）$y=-x^{2}+3.$

在二次函数 $ y = ax^{2} + k $ 中,$ a $,$ k $ 的值对抛物线 $ y = ax^{2} + k $ 的形状、位置有什么影响？

答案： $a$的符号决定抛物线$y=ax^{2}+k$的开口方向，$|a|$决定抛物线的开口大小，$k$的值决定抛物线$y=ax^{2}+k$的顶点在$y$轴上的位置.

1. 抛物线 $ y = \frac{1}{3}x^{2} + 4 $ 的对称轴是______,顶点坐标是______。

答案： $y$轴 $(0,4)$（解析：抛物线$y=ax^{2}+k$的对称轴是$y$轴，顶点为$(0,k).$）

2. 抛物线 $ y = \frac{1}{4}x^{2} $ 向______平移______个单位长度,可以得到抛物线 $ y = \frac{1}{4}x^{2} + 2 $。

答案： 上 2

3. 若抛物线 $ y = ax^{2} - 1 $ 经过点(4,31),则 $ a = $______,在这个函数图象上该点关于对称轴的对称点为______。

答案： 2 $(-4,31)$

4. 如果将抛物线 $ y = x^{2} + 2 $ 向下平移1个单位长度,那么所得到的新抛物线的解析式为( )。

A.$ y = (x - 1)^{2} + 2 $
B.$ y = (x + 1)^{2} + 2 $
C.$ y = x^{2} + 1 $
D.$ y = x^{2} + 3 $

答案： C

5. 若点($ x_{1} $,$ y_{1} $)和($ x_{2} $,$ y_{2} $)在二次函数 $ y = -\frac{1}{2}x^{2} - 2 $ 的图象上,且 $ x_{1} ＜ x_{2} ＜ 0 $,请讨论 $ y_{1} $ 与 $ y_{2} $ 的大小关系。

答案： 解：画出$y=-\dfrac{1}{2}x^{2}-2$的图象，易得$y_{1}\lt y_{2}.$

6. 图22.1 - 9是抛物线形拱桥,已知当水位在 $ AB $ 位置时,水面宽为 $ 4\sqrt{6} $ m,水位上升3 m,就到达警戒线 $ CD $,这时水面宽为 $ 4\sqrt{3} $ m。若建立如图22.1 - 9所示的坐标系,已知洪水到来后水位以0.25 m/h的速度上升。请解答下列各题：

(1)求点 $ B $,$ D $ 的坐标；
(2)求抛物线的解析式；
(3)求水位过警戒线后几小时淹到拱桥顶。

答案： 解：（1）点$B(2\sqrt{6},0)$，点$D(2\sqrt{3},3).$（2）设抛物线的解析式为$y=ax^{2}+k$，则有$\begin{cases}24a + k = 0,\\12a + k = 3,\end{cases}$解得$\begin{cases}a = -\dfrac{1}{4},\\k = 6.\end{cases}$故抛物线的解析式为$y=-\dfrac{1}{4}x^{2}+6.$（3）由题意，知$M(0,6)$，则$\dfrac{6 - 3}{0.25}=12$（h），即水位过警戒线后12h淹到拱桥顶.