《2025年实验班提优训练七年级数学上册浙教版》

12. 新情境 熔化铅球 (2024·安徽合肥五十中期中)把两个半径分别为 1cm 和$\sqrt[3]{7}cm$的铅球熔化后做成一个更大的铅球,则这个大铅球的半径是______cm(球的体积公式$V= \frac{4}{3}\pi r^3$,其中$r$是球的半径).
2

答案： 2　[解析]$\frac{4}{3}\pi× 1^3+\frac{4}{3}\pi× (\sqrt[3]{7})^3=\frac{32}{3}\pi(\text{cm}^3)$,
∴大铅球的半径为$\sqrt[3]{\frac{32}{3}\pi× \frac{3}{4}÷ \pi}=2(\text{cm})$.

13. (2025·山西吕梁期末)母亲节来临之际,小康和小明分别制作了一个正方体礼盒,准备用礼盒装好礼物送给妈妈. 已知小康制作的正方体礼盒的表面积为$150cm^2$,而小明制作的正方体礼盒的体积比小康制作的正方体礼盒小$61cm^3$,则小明制作的正方体礼盒的表面积为______$96\ \text{cm}^2$.

答案： $96\ \text{cm}^2$　[解析]设小康制作的正方体礼盒的边长为a cm,则$6a^2=150$,解得$a=5$,
∴小康制作的正方体礼盒的体积为$5^3=125(\text{cm}^3)$.
∵小明制作的正方体礼盒的体积比小康制作的正方体礼盒小$61\ \text{cm}^3$,
∴小明制作的正方体礼盒的体积为$125-61=64(\text{cm}^3)$,
∴小明制作的正方体礼盒的边长为$\sqrt[3]{64}=4(\text{cm})$,
∴小明制作的正方体礼盒的表面积为$6× 4^2=96(\text{cm}^2)$.

14. (2025·山东德州期中)若$\sqrt[3]{2y - 1}与\sqrt[3]{1 - 3x}$互为相反数,用含$x的式子表示y$.

答案： 根据题意,得$\sqrt[3]{2y-1}+\sqrt[3]{1-3x}=0$,
∴$\sqrt[3]{2y-1}=-\sqrt[3]{1-3x}$,
∴$2y-1=-1+3x$,
∴$y=\frac{3}{2}x$.

15. 已知$3m - 4与7 - 4m是N$的两个平方根,求$-2 - N$的立方根.

答案： 由题意,得$3m-4+7-4m=0$,解得$m=3$,则$N=(3× 3-4)^2=25$,所以$-2-N=-2-25=-27$,所以-27的立方根是-3,即$-2-N$的立方根是-3.

16. 请根据如图所示的对话内容回答下列问题.

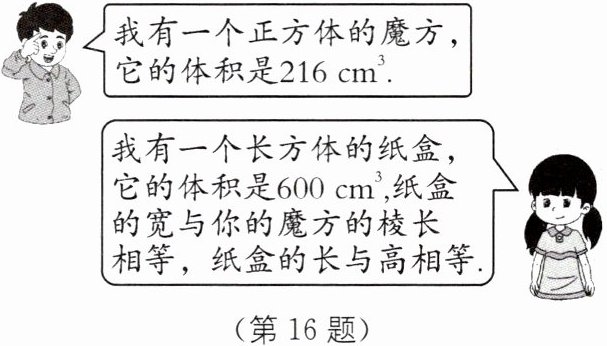
(1)求该魔方的棱长;
(2)求该长方体纸盒的表面积.

答案：
(1)设魔方的棱长为x cm,由题意,得$x^3=216$,解得$x=6$.故该魔方的棱长为6 cm.
(2)设该长方体纸盒的长为y cm,则$6y^2=600$,故$y^2=100$,解得$y=\pm 10$.因为y是正数，所以$y=10$,所以长方体纸盒的表面积为$10× 10× 2+10× 6× \4=440(\text{cm}^2)$.故该长方体纸盒的表面积为$440\ \text{cm}^2$.

17. 中考新考法 类比猜想 观察下列各式,然后探索下列问题:
$\because\sqrt[3]{1}= 1,\sqrt[3]{-1}= -1,\therefore\sqrt[3]{-1}= -\sqrt[3]{1}$.
$\because\sqrt[3]{8}= 2,\sqrt[3]{-8}= -2,\therefore\sqrt[3]{-8}= -\sqrt[3]{8}$.
$\because\sqrt[3]{27}= 3,\sqrt[3]{-27}= -3$,
$\therefore\sqrt[3]{-27}= -\sqrt[3]{27}$.
…
$\because\sqrt[3]{n^3}=$n,$\sqrt[3]{-n^3}=$-n,
$\therefore$$\sqrt[3]{-n^3}$=$-\sqrt[3]{n^3}$.
(1)在上面的“______”中填空,并猜测互为相反数的两个数的立方根有何关系;
(2)计算:$\sqrt[3]{-1}+\sqrt[3]{-8}+\sqrt[3]{-27}+…+\sqrt[3]{-100^3}$.
(1)猜测:互为相反数的两个数的立方根互为相反数.
(2)原式$=-1-2-3-\cdots -100=-5050$

答案：
(1)n -n $\sqrt[3]{-n^3}$ $-\sqrt[3]{n^3}$猜测:互为相反数的两个数的立方根互为相反数.
(2)原式$=-1-2-3-\cdots -100=-5050$.素养考向　本题主要考查了立方根,也考查了数学学科核心素养中的抽象能力,通过计算,得出互为相反数的两个数的立方根之间的关系,有利于培养学生的运算能力.

18. (2024·成都中考改编)若$m,n$为实数,且$(m + 4)^2+\sqrt{n - 5}= 0$,则$m + n$ 的立方根是______1.

答案： 1　[解析]
∵$(m+4)^2+\sqrt{n-5}=0$,
∴$m+4=0$,$n-5=0$,解得$m=-4$,$n=5$,
∴$m+n=1$,
∴$m+n$的立方根为1.