第123页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
1. (2025·江苏宿迁泗阳期末)如图.我们可借助圆规判断线段 AB 和 CD 的长短,由图可知(
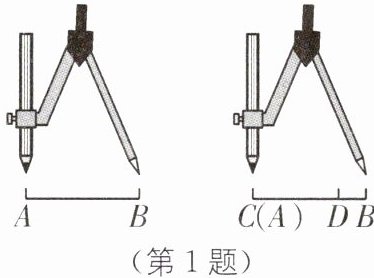
A.AB>CD
B.AB= CD
C.AB<CD
D.无法确定
A
).
A.AB>CD
B.AB= CD
C.AB<CD
D.无法确定
答案:
A
2. (2024·温州期末)如图,一骑马少年从 M 地出发,经过小溪 l 回到位于 N 地的家中,为使路程最短,则过小溪 l 的地方应选择(

A.A 地
B.B 地
C.C 地
D.D 地
C
).
A.A 地
B.B 地
C.C 地
D.D 地
答案:
C [解析]根据两点之间线段最短,得为使路程最短,则过小溪的地方应选择C地.故选C.
3. 教材 P172 作业题 T2·变式 如图,比较三角形三条边的长短,并用">"连接起来.


答案:
如图,作射线OE,分别在射线OE上截取OA'=AC,OB'=AB,OC'=BC.

由图可得,OA'>OC'>OB',即AC>BC>AB.
如图,作射线OE,分别在射线OE上截取OA'=AC,OB'=AB,OC'=BC.

由图可得,OA'>OC'>OB',即AC>BC>AB.
4. (2024·山东济宁期中)点 A,B,C 在直线 l 上的位置如图所示,下列结论中,不正确的是(
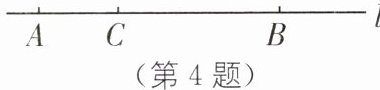
A.AB>AC
B.AB>BC
C.AC+BC= AB
D.AC>BC
D
).
A.AB>AC
B.AB>BC
C.AC+BC= AB
D.AC>BC
答案:
D [解析]A.由题图,得AB>AC,故A选项正确,不符合题意;
B.由题图,得AB>BC,故B选项正确,不符合题意;
C.由题图,得AC+BC=AB,故C选项正确,不符合题意;
D.由题图,得AC<BC,故D选项错误,符合题意.
故选D.
B.由题图,得AB>BC,故B选项正确,不符合题意;
C.由题图,得AC+BC=AB,故C选项正确,不符合题意;
D.由题图,得AC<BC,故D选项错误,符合题意.
故选D.
5. (2025·贵州贵阳期末)如图,AB= CD,则 AC 与 BD 的大小关系是(

A.AC>BD
B.AC<BD
C.AC= BD
D.无法确定
C
).
A.AC>BD
B.AC<BD
C.AC= BD
D.无法确定
答案:
C [解析]
∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD.故选C.
∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD.故选C.
6. (2025·四川德阳旌阳区期末)如图,用剪刀沿直线将一片平整的树叶剪掉一部分,则剩下的树叶周长小于原树叶的周长,能解释这一现象的数学道理是(

A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.经过一点有无数条直线
B
).
A.垂线段最短
B.两点之间线段最短
C.两点确定一条直线
D.经过一点有无数条直线
答案:
B
7. (2025·北京丰台区期末)小丰家准备自驾去抗日战争纪念馆.出发前,爸爸用地图软件查到导航路程为 11.3 千米.小丰用地图软件中的测距功能测出他家和目的地之间的距离为 9.3 千米,小丰发现他测得的距离比爸爸查到的导航路程少.用数学知识说明其中的道理:
两点之间线段最短
.
答案:
两点之间线段最短 [解析]由题意,得解释这一现象的数学知识最合理的是两点之间线段最短.
8. 有如图两条线段,比较其中 a,b 的长度,则结论是 a
=
b.(填">""<"或"=")
答案:
= [解析]借助刻度尺,分别量出两条线段的长度,再比较长短.
9. (2025·丽水莲都区期末改编)如图,已知线段 AB 和点 C,请用直尺和圆规作图(不要求写出作图过程,要保留作图痕迹).
(1)作射线 CA,直线 CB;
(2)比较大小:AC+AB______CB,依据是______.
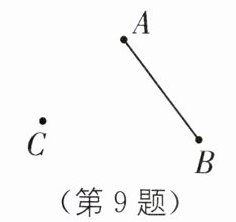
(1)作射线 CA,直线 CB;
(2)比较大小:AC+AB______CB,依据是______.

答案:
(1)如图,射线CA,直线BC即为所求.

(2)> 两点之间线段最短
(1)如图,射线CA,直线BC即为所求.

(2)> 两点之间线段最短
10. 转化思想 如图,要想从 A 村到 B 村,你能找到一条最近的路线吗?请说明理由.


答案:
能,最近的路线为A→C→F→B.理由如下:
因为从A村到C村的距离是固定的,所以从A村到B村的远近取决于C村到B村的距离.把C,B看成两个点,因为两点之间线段最短,且F在线段CB上,所以从C到F再到B最近,所以最近的路线为A→C→F→B.
因为从A村到C村的距离是固定的,所以从A村到B村的远近取决于C村到B村的距离.把C,B看成两个点,因为两点之间线段最短,且F在线段CB上,所以从C到F再到B最近,所以最近的路线为A→C→F→B.
11. 作图:已知线段 a,b,画一条线段 AB 使它等于 2a-b,简要说明作法.(要求:用尺规作图,保留作图痕迹)


答案:
如图所示,线段AC=2a - b即为所求作的线段,

AD=a,BD=a,以点B为起点,向反方向,即BA方向取BC=b,
∴AC=2a - b.
如图所示,线段AC=2a - b即为所求作的线段,

AD=a,BD=a,以点B为起点,向反方向,即BA方向取BC=b,
∴AC=2a - b.
12. (2025·台州临海期末)如图,已知平面内有线段 AB,BC 和点 D,且 AB≤BC,请按下列要求作图:
(1)作射线 AB,并在射线 AB 上取点 E,使得 BE= BC(请用无刻度 的直尺和圆规作图,并保留作图痕迹,不写作法); (2)在 BC 上取一点 F,使得 AF+DF 最短,并说明理由.

(1)作射线 AB,并在射线 AB 上取点 E,使得 BE= BC(请用无刻度 的直尺和圆规作图,并保留作图痕迹,不写作法); (2)在 BC 上取一点 F,使得 AF+DF 最短,并说明理由.

答案:
(1)如图,以点B为圆心,BC的长为半径画弧,交AB的延长线于点E,则点E即为所求.

(2)如图,连结AD交BC于点F,则点F即为所求.理由如下:两点之间线段最短.
方法诠释 解此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作,也考查了两点之间线段最短
(1)如图,以点B为圆心,BC的长为半径画弧,交AB的延长线于点E,则点E即为所求.

(2)如图,连结AD交BC于点F,则点F即为所求.理由如下:两点之间线段最短.
方法诠释 解此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作,也考查了两点之间线段最短
13. 最短路程模型如图所示为某风景区的旅游路线示意图,其中 B,C,D为风景点,E 为两条路的交叉点,图中数据为相应两点间的路程(单位:km).一学生从 A 处出发,以2km/h 的速度步行游览,每个景点的逗留时间均为0.h (1)当他沿着路线 A-D-C-E-A 游览回到 A 处时,共用了3h,求点 C,E 之间的路程. (2)若此学生打算从 A 处出发后,步行速度与在景点的逗留时间保持不变,且在最短时间内看完三个景点返回到 A 处,请你为他设计一条步行路线,并说明这样设计的理由.(不考虑其他因素)
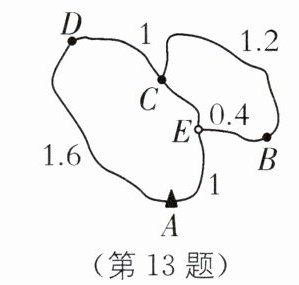

答案:
(1)设点C,E之间的路程为x km.
由题意,得1.6+1+x+1=(3 - 0.5×2)×2,
解得x=0.4,即点C,E之间的路程为0.4 km.
(2)由题图可知最佳路线为A—D—C—E—B—E—A或A—E—B—E—C—D—A.理由如下:
这样行走总路程最短.
(1)设点C,E之间的路程为x km.
由题意,得1.6+1+x+1=(3 - 0.5×2)×2,
解得x=0.4,即点C,E之间的路程为0.4 km.
(2)由题图可知最佳路线为A—D—C—E—B—E—A或A—E—B—E—C—D—A.理由如下:
这样行走总路程最短.
查看更多完整答案,请扫码查看


