第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
17.中考新考法 过程纠错改错 (2025·杭州萧山区期中)方方同学计算$-4^{2}÷(-2)^{3}×(-\frac {1}{8})$的过程如下:
方方:$-4^{2}÷(-2)^{3}×(-\frac {1}{8})$ $=-16÷(-8)×(-\frac {1}{8})$…………① $=-16÷[(-8)×(-\frac {1}{8})]$…………② $=-16÷1$…………③ $=-16$.…………④
(1)以上计算过程中,方方是第
方方:$-4^{2}÷(-2)^{3}×(-\frac {1}{8})$ $=-16÷(-8)×(-\frac {1}{8})$…………① $=-16÷[(-8)×(-\frac {1}{8})]$…………② $=-16÷1$…………③ $=-16$.…………④
(1)以上计算过程中,方方是第
②
步开始出错(填序号). (2)写出正确计算过的程.$-4^{2}÷(-2)^{3}×(-\frac {1}{8})=-16÷(-8)×(-\frac {1}{8})=-16×(-\frac {1}{8})×(-\frac {1}{8})=-\frac {1}{4}$
答案:
17.
(1)②
(2)-4²÷(-2)³×(-$\frac{1}{8}$)=-16÷(-8)×(-$\frac{1}{8}$)=-16×(-$\frac{1}{8}$)×(-$\frac{1}{8}$)=-$\frac{1}{4}$.
(1)②
(2)-4²÷(-2)³×(-$\frac{1}{8}$)=-16÷(-8)×(-$\frac{1}{8}$)=-16×(-$\frac{1}{8}$)×(-$\frac{1}{8}$)=-$\frac{1}{4}$.
18.我们知道$\frac {1}{22}= \frac {1}{2}×\frac {1}{11},\frac {1}{33}= \frac {1}{3}×\frac {1}{11},\frac {1}{44}= \frac {1}{4}×\frac {1}{11}$,你能计算$\frac {1}{22}-\frac {1}{33}+\frac {1}{44}-\frac {1}{55}$吗?$\frac {1}{22}+\frac {1}{66}+\frac {1}{132}+\frac {1}{220}$怎么计算呢?
答案:
18.$\frac{1}{22}$-$\frac{1}{33}$+$\frac{1}{44}$-$\frac{1}{55}$=$\frac{1}{2}$×$\frac{1}{11}$-$\frac{1}{3}$×$\frac{1}{11}$+$\frac{1}{4}$×$\frac{1}{11}$-$\frac{1}{5}$×$\frac{1}{11}$=$\frac{1}{11}$×($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{4}$-$\frac{1}{5}$)=$\frac{13}{660}$;
$\frac{1}{22}$+$\frac{1}{66}$+$\frac{1}{132}$+$\frac{1}{220}$=$\frac{1}{2}$×$\frac{1}{11}$+$\frac{1}{6}$×$\frac{1}{11}$+$\frac{1}{12}$×$\frac{1}{11}$+$\frac{1}{20}$×$\frac{1}{11}$=$\frac{1}{11}$×($\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$)=$\frac{1}{11}$×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$)=$\frac{1}{11}$×(1-$\frac{1}{5}$)=$\frac{4}{55}$.
归纳总结 本题主要考查了有理数的混合运算中的乘法分配律,熟练掌握分配律是解本题的关键.
$\frac{1}{22}$+$\frac{1}{66}$+$\frac{1}{132}$+$\frac{1}{220}$=$\frac{1}{2}$×$\frac{1}{11}$+$\frac{1}{6}$×$\frac{1}{11}$+$\frac{1}{12}$×$\frac{1}{11}$+$\frac{1}{20}$×$\frac{1}{11}$=$\frac{1}{11}$×($\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{20}$)=$\frac{1}{11}$×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$)=$\frac{1}{11}$×(1-$\frac{1}{5}$)=$\frac{4}{55}$.
归纳总结 本题主要考查了有理数的混合运算中的乘法分配律,熟练掌握分配律是解本题的关键.
19. (1)在玩“24点游戏时,” “3,3,7,7”列式并计算为$7×(3+\frac {3}{7})= 7×3+3= 24$是依据运算律:
(2)小明抽到以下4张牌,如图:
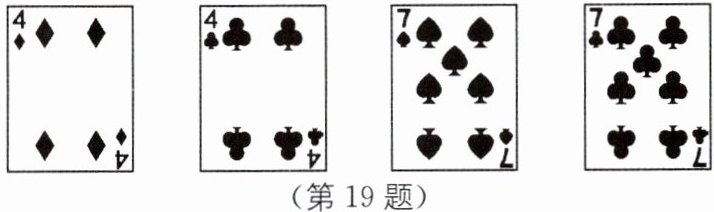
请你帮他写出运算结果为24的一个算式;
(3)如果$◆$表示正,$♣$表示负,请你用(2)中的4张牌表示的数写出运算结果为24的一个算式.
乘法分配律
;(2)小明抽到以下4张牌,如图:

请你帮他写出运算结果为24的一个算式;
7×(4-$\frac{4}{7}$)
(3)如果$◆$表示正,$♣$表示负,请你用(2)中的4张牌表示的数写出运算结果为24的一个算式.
-7×(-$\frac{4}{7}$-4)
答案:
19.
(1)乘法分配律
(2)7×(4-$\frac{4}{7}$)(答案不唯一)
(3)-7×(-$\frac{4}{7}$-4)(答案不唯一)
(1)乘法分配律
(2)7×(4-$\frac{4}{7}$)(答案不唯一)
(3)-7×(-$\frac{4}{7}$-4)(答案不唯一)
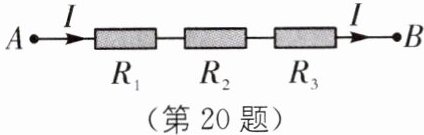
20. 跨学科 电路 (2024·广州中考)如图,把$R_{1},R_{2},R_{3}$三个电阻串联起来,线路AB上的电流为I,电压为U,则$U= IR_{1}+IR_{2}+IR_{3}$,当$R_{1}= 20.3,R_{2}= 31.9,R_{3}= 47.8,I= 2.2$时,U的值为______.

220
答案:
20. 220 [解析]由题意,得U=IR₁+IR₂+IR₃=2.2×20.3+2.2×31.9+2.2×47.8=2.2×(20.3+31.9+47.8)=220.
方法诠释 本题考查有理数的混合运算,新定义,解答本题的关键是明确题意,利用新定义解答.
方法诠释 本题考查有理数的混合运算,新定义,解答本题的关键是明确题意,利用新定义解答.
查看更多完整答案,请扫码查看


