《2025年实验班提优训练七年级数学上册浙教版》

1. (2025·温州期末)将一副三角板按如图所示摆放,已知∠α的度数为55°,则∠β的度数为(C).

A.35°
B.45°
C.55°
D.60°

答案： C [解析]
∵∠α+∠1=90°,∠β+∠1=90°,
∴∠β=∠α=55°.故选 C.

2. (2025·温州苍南期末)如图,C 是直线 AB 上一点,CE,CF 分别是∠ACD,∠BCD 的平分线. 若∠BCF 的度数为 28°,则∠ACE 的度数是(B).

A.56°
B.62°
C.72°
D.84°

答案： B

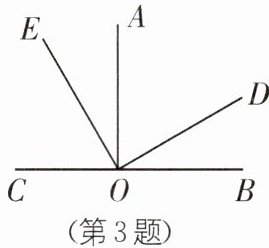
3. 如图,点 C,O,B 在同一条直线上,∠AOB= 90°,∠AOE= ∠DOB,则下列结论：①∠EOD= 90°；②∠COE= ∠AOD；③∠COE= ∠DOB；④∠COE+∠BOD= 90°；⑤∠COE+∠AOD= 90°. 其中正确的个数是(C).

A.1
B.2
C.3
D.4

答案： C [解析]
∵∠AOB=90°,
∴∠AOD+∠BOD=90°.
∵∠AOE=∠DOB,
∴∠AOE+∠AOD=90°,即∠EOD=90°.
∵∠AOB=90°,
∴∠AOC=90°,
∴∠AOE+∠COE=90°.又∠AOE+∠AOD=90°,
∴∠COE=∠AOD,
∴∠COE+∠BOD=90°.故①②④正确,③⑤错误.故正确的个数是 3.故选 C.

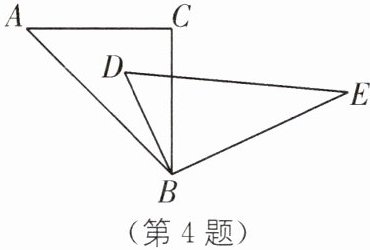
4. (2025·湖州期末)一副三角板如图所示摆放,若∠ABE= 110°,则∠DBC 等于(B).

A.20°
B.25°
C.15°
D.30°

答案： B

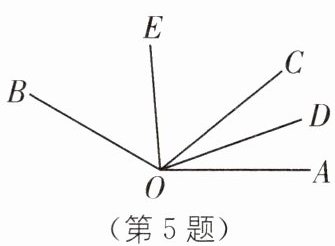
5. 教材 P186 作业题 T4·变式 (2025·天津西青区期末)如图,在∠AOB 内部任意画一条射线 OC,OD 平分∠AOC,OE 平分∠BOC,若∠AOB= 150°,则∠EOD 的度数为75°.

答案： 75° [解析]
∵OD 平分∠AOC,OE 平分∠BOC,
∴∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}$∠BOC,
∴∠EOD=∠EOC+∠COD=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$∠AOB.
∵∠AOB=150°,
∴∠EOD=$\frac{1}{2}$∠AOB=75°.

6. 方程思想 如图,点 O 在直线 MN 上,过点 O 作射线 OA 和 OB,已知∠MOA= 2∠BON,∠BON 比∠AOB 大 20°,求∠MOA 和∠AOB 的度数.

答案： 设∠BON=x°,则∠MOA=2x°.由题意,得 x-(180-x-2x)=20,解得 x=50,所以∠MOA=2x°=100°,所以∠AOB=180°-x°-2x°=30°.

7. 分类讨论思想 (2024·广东深圳期末)已知∠AOB= 58°32′,以 O 为端点作射线 OC,使∠AOC= 42°41′,则∠BOC 的度数为( ).

A.15°51′
B.101°13′
C.15°51′或 101°13′
D.16°51′或 101°13′

答案：
C [解析] ①如图
(1),当射线 OC 在射线 OA 右侧时,∠BOC=∠AOB+∠AOC=58°32'+42°41'=101°13';
　　　　
②如图
(2),当射线 OC 在射线 OA 左侧时,∠BOC=∠AOB-∠AOC=58°32'-42°41'=15°51'.综上所述,∠BOC 的度数是 101°13'或 15°51'.故选 C.易错警示 本题考查角的计算,关键是要分两种情况讨论.

8. (2025·黑龙江绥化海伦期末)如图,将一张长方形纸片 ABCD 分别沿着 BE,BF 折叠,使边 AB,CB 均落在 BD 上,得到折痕 BE,BF,则∠EBF 等于(C).

A.30°
B.35°
C.45°
D.60°

答案： C [解析] 由折叠,知∠CBF=∠DBF,∠ABE=∠DBE,
∴∠DBF=$\frac{1}{2}$∠CBD,∠DBE=$\frac{1}{2}$∠ABD,→折叠可理解为作角平分线
∴∠EBF=∠DBF+∠DBE=$\frac{1}{2}$∠CBD+$\frac{1}{2}$∠ABD=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×90°=45°.故选 C.

9. 分类讨论思想 如图,已知∠AOB= 45°,射线 OM 从 OA 出发,以每秒 5°的速度在∠AOB 内部绕点 O 逆时针旋转,若∠AOM 和∠BOM 中,有一个角是另一个角的 2 倍,则运动时间为3 或 6秒.

答案： 3 或 6 [解析] 设运动时间为 t 秒,此时∠AOM=(5t)°,∠BOM=(45-5t)°.当∠BOM=2∠AOM 时,由题意,得 45-5t=2×5t,解得 t=3;当∠AOM=2∠BOM 时,由题意,得 5t=2(45-5t),解得 t=6.综上所述,运动时间为 3 或 6 秒.素养考向 本题由于给出“有一个角是另一个角的 2 倍”不确定这两个角的大小关系,要分两种情况讨论,体现了分类讨论思想的运用.