《2025年实验班提优训练七年级数学上册浙教版》

10.(2025·四川绵阳游仙区期中)的士司机张师傅一天以中英文站为出发点在东西方向营运,向东为正,向西为负.行车里程(单位：km),依先后次序记录如下：+8,-3,-4,+6,-5,+4,+2,-3.
(1)张师傅将最后一名乘客送到目的地时,此车离中英文站多远？在中英文站的什么方向？
(2)若每行驶 1 km 耗油 0.5 升,这天这辆车耗油多少升？

答案：
(1)+8+(−3)+(−4)+6+(−5)+4+2+(−3)=5(km).故张师傅将最后一名乘客送到目的地时，此车离中英文站5km,在中英文站东面.
(2)|+8|+|−3|+|−4|+|+6|+|−5|+|+4|+|+2|+|−3|=35(km),35×0.5=17.5(升).故这天这辆车耗油17.5升.
归纳总结　解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量，在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示.

11.规律探究：
计算：$1+2+3+4+…+99+100$.
如果一个个顺次相加显然太繁杂,我们仔细观察这个式子的特点,发现运用加法的运算律,可简化计算,提高计算速度.
$1+2+3+4+…+99+100= (1+100)+(2+99)+…+(50+51)= 5050$.
计算：
(1)$3+5+7+9+…+101$；
(2)$2+4+6+8+…+98+100$.

答案：
(1)原式=(3+101)×25=2600.
(2)原式=(2+100)×25=2550.
知识拓展　本题主要考查有理数的加法和数字的规律，解题的关键是得出式子的特点：前后对应的两个数的和相等，并熟练掌握有理数的运算法则.

12.(2024·陕西中考)小华探究“幻方”时,提出了一个问题：如图,将 0,-2,-1,1,2 这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是______.(写出一个符合题意的数即可)

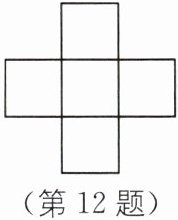
答案：
0(答案不唯一) [解析]由题意，填写如下:

1+0+(−1)=0,2+0+(−2)=0,满足题意.
思路引导　本题考查了有理数的运算，根据横向三个数之和与纵向三个数之和相等，进行填写即可得出结果.