2025年快乐暑假黄山书社八年级数学沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假黄山书社八年级数学沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
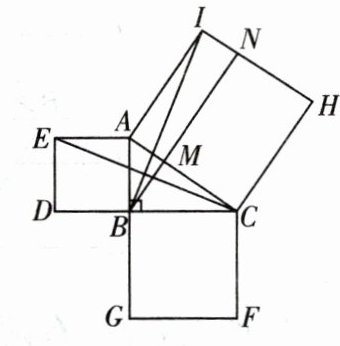
11. 欧几里得是古希腊著名的数学家、欧氏几何的开创者.下面问题是欧几里得证明勾股定理的证法的一小片段:如图,在$Rt△ABC$中,$∠ABC=90^{\circ }$,分别以$Rt△ABC$的三边为边长,向外作正方形 ABDE,BCFG,ACHI.
(1) 连接 BI,CE,若$AB=2,BC=3$,求 BI 的长.
(2) 过点 B 作$BN// AI$,交 AC 于点 M,交 HI 于点 N.若$AI=4,NI=1$,则正方形 BCFG 的边长是多少?
(1) 连接 BI,CE,若$AB=2,BC=3$,求 BI 的长.
$\sqrt{29}$
(2) 过点 B 作$BN// AI$,交 AC 于点 M,交 HI 于点 N.若$AI=4,NI=1$,则正方形 BCFG 的边长是多少?
2$\sqrt{3}$

答案:
11.
(1) $\sqrt{29}$
(2)2$\sqrt{3}$
(1) $\sqrt{29}$
(2)2$\sqrt{3}$
12. 如图,$△ABC$和$△DCE$都是等腰直角三角形,$∠ACB=∠DCE=90^{\circ }$.
(1) 如图,探索 BE 与 AD 之间的数量关系和位置关系;
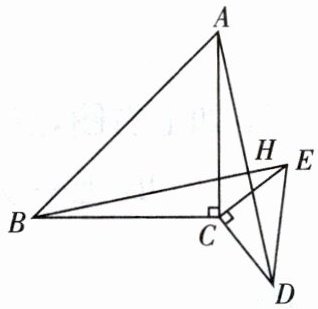
(2) 如图,当 A,E,D 三点在同一直线上时,$AE=1,AC=\sqrt {5}$,求 BD 的长;
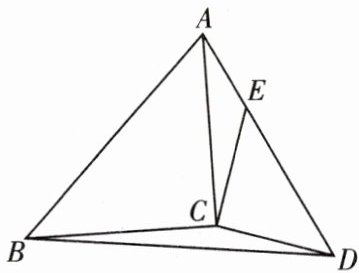
(3) 如图,以等腰$Rt△ABC$的腰 AC 为直角边作$Rt△ACD$,且$∠DAC=90^{\circ },CD=8$,连接 BD,求 BD 的最大值;
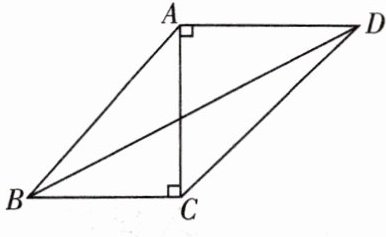
(1) 如图,探索 BE 与 AD 之间的数量关系和位置关系;
BE = AD,BE⊥AD

(2) 如图,当 A,E,D 三点在同一直线上时,$AE=1,AC=\sqrt {5}$,求 BD 的长;
$\sqrt{13}$

(3) 如图,以等腰$Rt△ABC$的腰 AC 为直角边作$Rt△ACD$,且$∠DAC=90^{\circ },CD=8$,连接 BD,求 BD 的最大值;
4 + $\sqrt{5}$

答案:
12.
(1)BE = AD,BE⊥AD.
(2)BD = $\sqrt{13}$
(3)4 + $\sqrt{5}$
(1)BE = AD,BE⊥AD.
(2)BD = $\sqrt{13}$
(3)4 + $\sqrt{5}$
查看更多完整答案,请扫码查看


