《2025年快乐暑假黄山书社八年级数学沪科版》

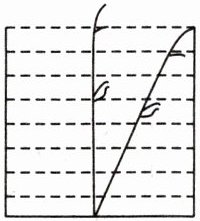
6. 我国古代数学著作《九章算术》中有这样一个问题：“今有池方一丈，葭（jiā）生其中央，出水一尺。引葭赴岸，适与岸齐。问水深几何？”（注：丈、尺是长度单位，$1$丈$= 10$尺）这段话翻译成现代汉语就是：有一个水池，水面是一个边长为$1$丈的正方形，在水池正中央有一根芦苇，它高出水面$1$尺。如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，则水池里水的深度是12尺。（如下左图）

答案： 12

7. 一种盛饮料的圆柱形杯，内部底面半径为$2.5cm$，高为$12cm$。把吸管放进杯里（如上右图所示），杯口外面至少要露出$4.6cm$。为节省材料，管长$a$的取值范围是$16.6 \mathrm{cm} \leq a \leq 17.6 \mathrm{cm} $。

答案： $16.6 \mathrm{cm} \leq a \leq 17.6 \mathrm{cm} $

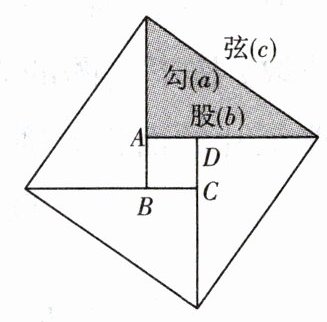
8. 公元$3$世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”。如下左图，设勾$a = 6$，弦$c = 10$，则小正方形$ABCD$的面积是4。

答案： 4

9. 如上右图，在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$CA = CB = 3$，点$D$在边$BC$上。将$Rt\triangle ACD$沿$AD$折叠，使点$C$落在点$C'$处，连接$BC'$，则$BC'$的最小值为__________$3 \sqrt{2} - 3$。

答案： $3 \sqrt{2} - 3 $ [提示:易求 $AB = 3 \sqrt{2} $，$AC ^ { \prime } = AC = 3 $，$\because BC ^ { \prime } \geq AB - AC ^ { \prime } $，$\therefore $ 当 $A$，$C ^ { \prime }$，$B$ 三点在同一条直线上时，$BC ^ { \prime }$ 最小，最小值为 $BC ^ { \prime } = AB - AC ^ { \prime } = 3 \sqrt{2} - 3 $。]

10. 已知关于$x$，$y$的方程组$\begin{cases}ax + 2\sqrt{3}y = - 10\sqrt{3},\\x + y = 4\end{cases}$与$\begin{cases}x - y = 2,\\x + by = 15\end{cases}$的解相同。
（1）求$a$，$b$的值；
（2）若一个三角形的一条边的长为$2\sqrt{6}$，另外两条边的长是关于$x$的方程$x^{2}+ax + b = 0$的解，试判断该三角形的形状，并说明理由。
（1）$a=$$-4\sqrt{3}$，$b=$$12$；
（2）该三角形是等腰直角三角形。

答案： $(1)$求$a$，$b$的值
因为两个方程组的解相同，所以先求解方程组$\begin{cases}x + y = 4 \\x - y = 2 \end{cases}$。
将两个方程相加消去$y$可得：
$(x + y)+(x - y)=4 + 2$
$x + y+x - y=6$
$2x=6$，解得$x = 3$。
把$x = 3$代入$x + y = 4$，得$3 + y = 4$，解得$y = 1$。
把$x = 3$，$y = 1$代入$ax + 2\sqrt{3}y = - 10\sqrt{3}$，得$3a+2\sqrt{3}\times1=-10\sqrt{3}$，
$3a=-10\sqrt{3}-2\sqrt{3}$，
$3a=-12\sqrt{3}$，解得$a=-4\sqrt{3}$。
把$x = 3$，$y = 1$代入$x + by = 15$，得$3 + b\times1 = 15$，解得$b = 12$。
$(2)$判断三角形的形状
已知方程$x^{2}+ax + b = 0$，将$a=-4\sqrt{3}$，$b = 12$代入方程得$x^{2}-4\sqrt{3}x + 12 = 0$。
对于一元二次方程$mx^{2}+nx+p = 0$（$m\neq0$），其判别式$\Delta=n^{2}-4mp$，在方程$x^{2}-4\sqrt{3}x + 12 = 0$中，$m = 1$，$n=-4\sqrt{3}$，$p = 12$，则$\Delta=(-4\sqrt{3})^{2}-4\times1\times12$
$=48 - 48=0$。
根据求根公式$x=\frac{-n\pm\sqrt{\Delta}}{2m}$，可得$x=\frac{4\sqrt{3}\pm\sqrt{0}}{2}=\frac{4\sqrt{3}}{2}=2\sqrt{3}$，所以方程$x^{2}-4\sqrt{3}x + 12 = 0$的两个根相等，都为$2\sqrt{3}$。
因为$(2\sqrt{3})^{2}+(2\sqrt{3})^{2}=12 + 12 = 24=(2\sqrt{6})^{2}$，满足勾股定理$a^{2}+b^{2}=c^{2}$（其中$a=b = 2\sqrt{3}$，$c = 2\sqrt{6}$），所以该三角形是等腰直角三角形。
综上，$(1)$$\boldsymbol{a=-4\sqrt{3}}$，$\boldsymbol{b = 12}$；$(2)$该三角形是**等腰直角三角形**。