第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
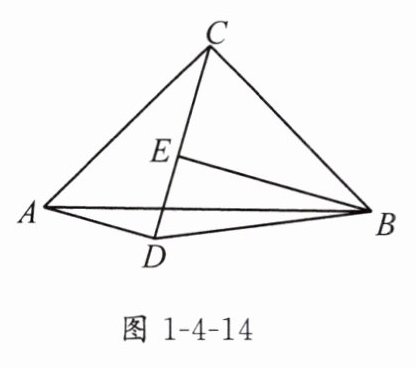
6. 如图1-4-14,△ABC是等腰直角三角形,∠BCA = 90°,AC = BC,AD⊥CD,BE⊥CD,垂足分别为点D,E.
(1)求证:AD = CE.
(2)连接BD,若BE平分∠DBC.
①试判断△DBC的形状,并给出证明过程;
②若CE = 4,则△ABD的面积 = ________.
(1)求证:AD = CE.
(2)连接BD,若BE平分∠DBC.
①试判断△DBC的形状,并给出证明过程;
②若CE = 4,则△ABD的面积 = ________.

答案:
(1)证明:因为AD⊥CD,BE⊥CD,所以∠ADC = ∠BEC = 90°。因为∠ACB = 90°,所以∠ACD + ∠BCE = 90°。又因为∠ACD + ∠CAD = 90°,所以∠CAD = ∠BCE。在△ACD和△CBE中,
$\begin{cases}∠ADC = ∠CEB,\\∠CAD = ∠BCE,\\AC = CB,\end{cases}$
所以△ACD≌△CBE(AAS)。所以AD = CE。
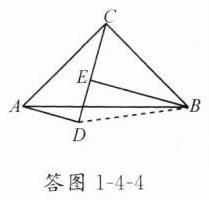
(2)解: ①△DBC为等腰三角形。证明:如答图1 - 4 - 4,因为BE⊥CD,所以∠BEC = ∠BED = 90°。因为∠EBC = ∠EBD,∠EBC + ∠BCE = 90°,∠EBD + ∠BDC = 90°,所以∠BCD = ∠BDC,所以BD = BC,所以△DBC为等腰三角形。 ②8 解析:因为△ACD≌△CBE,所以AD = EC = 4,EB = CD = 8,所以AC = BC = √(AD² + CD²)= 4√5,所以$S_{△ADB} = S_{△ADC} + S_{△BDC} - S_{△ACB}$ = 1/2×4×8 + 1/2×8×8 - 1/2×4√5×4√5 = 8。
(1)证明:因为AD⊥CD,BE⊥CD,所以∠ADC = ∠BEC = 90°。因为∠ACB = 90°,所以∠ACD + ∠BCE = 90°。又因为∠ACD + ∠CAD = 90°,所以∠CAD = ∠BCE。在△ACD和△CBE中,
$\begin{cases}∠ADC = ∠CEB,\\∠CAD = ∠BCE,\\AC = CB,\end{cases}$
所以△ACD≌△CBE(AAS)。所以AD = CE。
(2)解: ①△DBC为等腰三角形。证明:如答图1 - 4 - 4,因为BE⊥CD,所以∠BEC = ∠BED = 90°。因为∠EBC = ∠EBD,∠EBC + ∠BCE = 90°,∠EBD + ∠BDC = 90°,所以∠BCD = ∠BDC,所以BD = BC,所以△DBC为等腰三角形。 ②8 解析:因为△ACD≌△CBE,所以AD = EC = 4,EB = CD = 8,所以AC = BC = √(AD² + CD²)= 4√5,所以$S_{△ADB} = S_{△ADC} + S_{△BDC} - S_{△ACB}$ = 1/2×4×8 + 1/2×8×8 - 1/2×4√5×4√5 = 8。

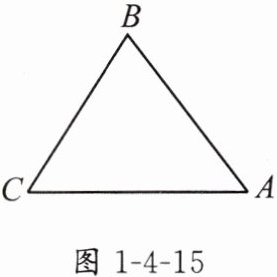
1. 如图1-4-15,现要在三角形地ABC内建一中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.

答案:
如答图1 - 4 - 5,用尺规作线段AB的垂直平分线,作∠BAC的平分线,根据线段垂直平分线、角平分线性质可知两线交点即为中心医院的位置。

如答图1 - 4 - 5,用尺规作线段AB的垂直平分线,作∠BAC的平分线,根据线段垂直平分线、角平分线性质可知两线交点即为中心医院的位置。

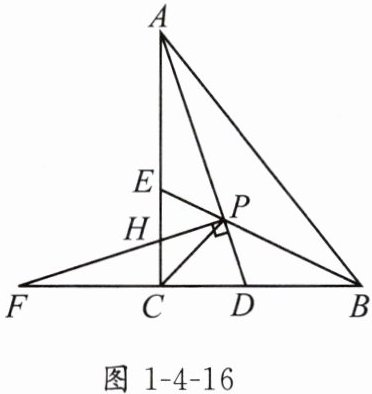
2. 如图1-4-16,在△ACB中,∠ACB = 90°,△ABC的角平分线AD,BE相交于点P,过点P作PF⊥AD交BC的延长线于点F,交AC于点H,给出下列结论:①连接CP,CP平分∠ACB;②∠APB = 135°;③PH = PD;④BF = BA. 其中正确的是________. (填序号)

答案:
①②③④
3. 如图1-4-17,在△ABC中,AB = 5,AC = 13,BC = 12,∠BAC与∠ACB的平分线相交于点D,点M,N分别在边AB,BC上,连接MN,当∠MDN = 45°时,求△BMN的周长.
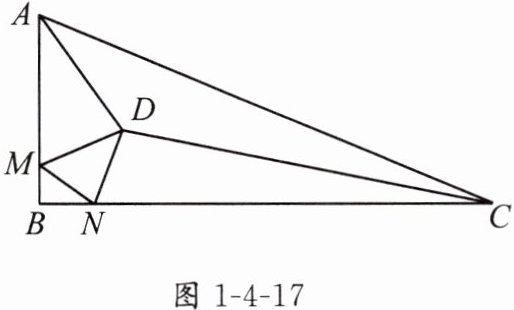

答案:
解:如答图1 - 4 - 6,由AB² + BC² = AC²,知∠ABC = 90°。过点D作DE⊥AB于点E,DF⊥BC于点F,DH⊥AC于点H,因为DA平分∠BAC,所以DE = DH,同理可得DF = DH,所以DE = DF。连接BD,则BD是∠ABC的平分线,所以△BED,△BFD为等腰直角三角形,所以BE = BF = DE = DF,即四边形BEDF为正方形。在Rt△ADE和Rt△ADH中,
$\begin{cases}AD = AD,\\DE = DH,\end{cases}$
所以Rt△ADE≌Rt△ADH(HL),所以AE = AH,同理可得Rt△CDF≌Rt△CDH(HL),所以CF = CH。设正方形BEDF的边长为x,则AE = AH = 5 - x,CF = CH = 12 - x。因为AH + CH = AC,所以5 - x + 12 - x = 13,解得x = 2,即BE = 2。在FC上截取FP = EM,连接DP,因为DE = DF,∠DEM = ∠DFP,EM = FP,所以△DEM≌△DFP(SAS),所以DM = DP,∠EDM = ∠FDP,所以∠MDP = ∠EDF = 90°。因为∠MDN = 45°,所以∠PDN = 45°。在△DMN和△DPN中,
$\begin{cases}DM = DP,\\∠MDN = ∠PDN,\\DN = DN,\end{cases}$
所以△DMN≌△DPN(SAS),所以MN = NP = NF + FP = NF + EM,所以△BMN的周长 = MN + BM + BN = EM + BM + BN + NF = BE + BF = 2 + 2 = 4。
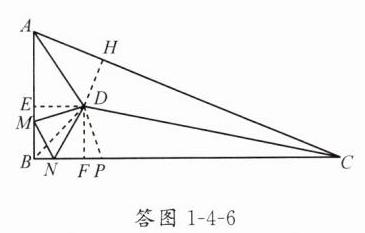
解:如答图1 - 4 - 6,由AB² + BC² = AC²,知∠ABC = 90°。过点D作DE⊥AB于点E,DF⊥BC于点F,DH⊥AC于点H,因为DA平分∠BAC,所以DE = DH,同理可得DF = DH,所以DE = DF。连接BD,则BD是∠ABC的平分线,所以△BED,△BFD为等腰直角三角形,所以BE = BF = DE = DF,即四边形BEDF为正方形。在Rt△ADE和Rt△ADH中,
$\begin{cases}AD = AD,\\DE = DH,\end{cases}$
所以Rt△ADE≌Rt△ADH(HL),所以AE = AH,同理可得Rt△CDF≌Rt△CDH(HL),所以CF = CH。设正方形BEDF的边长为x,则AE = AH = 5 - x,CF = CH = 12 - x。因为AH + CH = AC,所以5 - x + 12 - x = 13,解得x = 2,即BE = 2。在FC上截取FP = EM,连接DP,因为DE = DF,∠DEM = ∠DFP,EM = FP,所以△DEM≌△DFP(SAS),所以DM = DP,∠EDM = ∠FDP,所以∠MDP = ∠EDF = 90°。因为∠MDN = 45°,所以∠PDN = 45°。在△DMN和△DPN中,
$\begin{cases}DM = DP,\\∠MDN = ∠PDN,\\DN = DN,\end{cases}$
所以△DMN≌△DPN(SAS),所以MN = NP = NF + FP = NF + EM,所以△BMN的周长 = MN + BM + BN = EM + BM + BN + NF = BE + BF = 2 + 2 = 4。

查看更多完整答案,请扫码查看


